Introduction to Pose Space Deformation

Limitations of other methods

Limitations of Skinning

Weighted sums of rigid transformation matrices are not rigid transformation matrices.
$$ p_{transformed} = \underbrace{\sum_i w_iM_i(t) M_i^{-1}(0)}_\text{not a rigid matrix} p $$
This results in collapse artifacts:


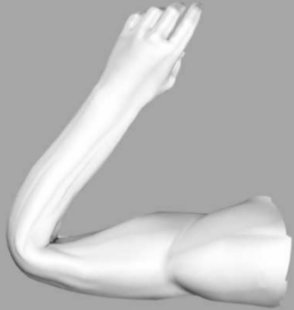
Bending: elbow collapse	Twisting: candy wrapper effect

Moreover, it is hard, if not impossible, to design joints with plausible deformations in a large range. The following image shows armpit bulging occuring while the arm is lift far above the reference position.

Armpit bulging

Even Dual Quaternion Skinning creates artefacts in bending:

Bulging artefact in Dual Quaternion Skinning (courtesy of L.Kavan)

Limitations of Blendshape Interpolation

Blendshape interpolation is more accumulation than interpolation.
$$ \begin{equation} \label{eq:blend shapes}
S = \sum_i w_i S_i
\end{equation}
$$
where $i$ spans the number of example shapes. The limitations are:

There are as many dimensions (sliders to tune) as example shapes.
Example shapes interfere with each other:

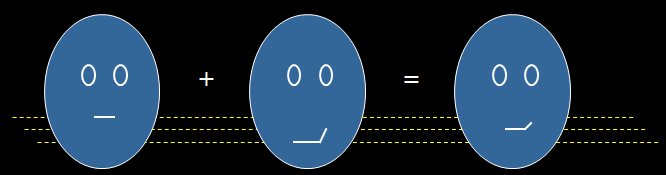Blendshape artefact: smirk counteracts raise. (courtesy of J.P.Lewis talk slides)

Motivation: Decoupling Modeling from Animation Control

The goal of Pose Space Deformation is to decouple animation control (pose space, i.e. control sliders) from modeling (example shapes). In the following example, the control space has two dimensions, while five examples are used to define the interpolation.

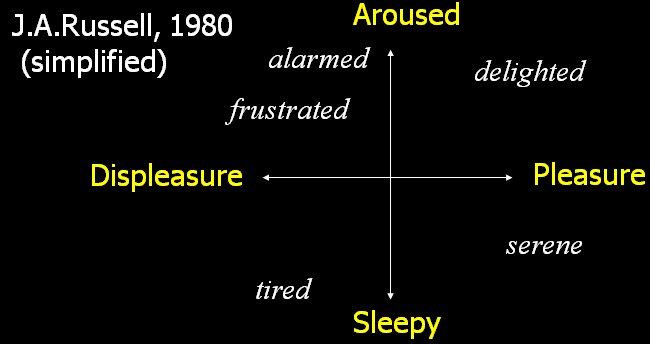Example of two-dimensional pose space in facial animation.

This requires mathematical tools to interpolate shapes based on an arbitrary, uneven distribution of samples: scattered interpolation.
For $p$ poses and $n$ vertices in 3d, RBF interpolation requires the factoring of a $p\times p$ matrix, and then the associated solution of $3n$ equation systems at initialization time. During run-time, each interpolation requires the evaluation of a formula similar to (\ref{eq:blend shapes}), where $i$ spans the dimensions of the pose space.

Layering PSD on an existing animation system

PSD can be used to interpolate corrections to an underlying shape computed using an other technique, e.g. skinning. The pose space is the parameter space of the underlying surface, e.g. joint angles. Displacements can be stored in a local frame.

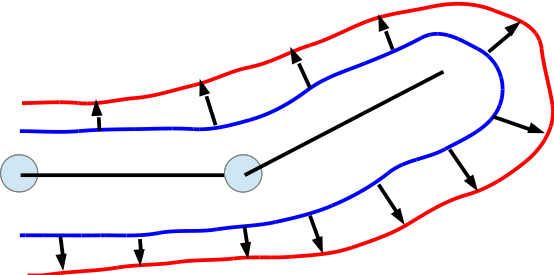PSD layered on skinning.

PSD has been used in facial animation to superimpose fine wrinkles on top of a coarse, physically-based face deformation.

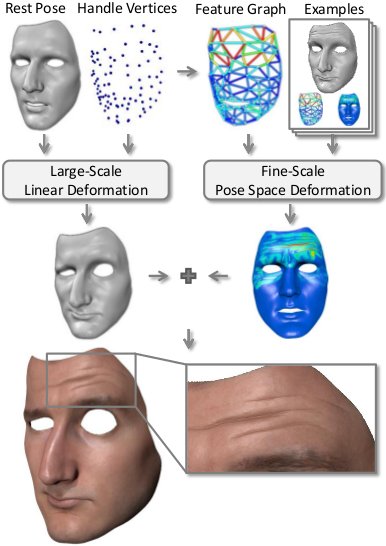Hybrid face animation pipeline.

The pose space is composed of mesh edge stretches, which are correlated to wrinkles. The distance to the samples is defined on a per-vertex basis as:
$$
\| f-f_j\|_v = \sqrt{ \sum_{i=1}^{F} \alpha_{v,i}( f_i - f_{i,j} )^2 }
$$
where $v$ is the vertex index, $F$ the number of examples, and $f_{i,j}$ is the strain of the $i$'th feature edge in the $j$'th pose. The weights $\alpha$ are assigned based on proximity to the feature edges as illustrated in the following figure.

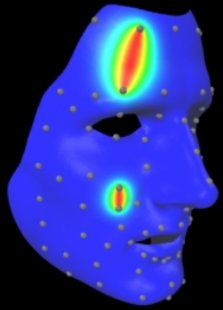Weight kernel used to compute per-vertex distance.

Francois Faure, University of Grenoble. Main page