[
A Bloch-Torrey Equation for Diffusion in a Deforming Media
Damien Rohmer, Grant T. Gullberg
The authors are with the Division of Life Science, E.O. Lawrence National Berkeley Laboratory,
1 Cyclotron Road, Berkeley, CA 94720, USA.

]
2DIFFUSION phenomenon is a macroscopic observation of the microscopic structure of the material in which it occurs. Knowledge of this diffusion in cases of various biological tissues such as cardiac muscle [1,2,3,4,5] , skeletal muscles [6,7,8,9], brain [10,11,12,13], tongue [14,15,16], spinal cord [17,18] or other [19] is therefore a probe into their intrinsic structures. Diffusion measurement using the Diffusion Tensor Magnetic Resonance Imaging (DTMRI) technique is a powerful tool for exploring the microscopic structure of tissues. This technique is well established for static cases and is widely used in brain imaging where the change in the diffusion coefficient is related to brain diseases [20,21,22].
Its utilization for other organs are currently in the research process and one of the most challenging applications is using the DTMRI technique on a living heart.
The fast and complex motion of the heart [23] prevents accurate measurements of the diffusion parameters. Static acquisitions of diffusion measurements on an ex-vivo heart have already demonstrated the value of measuring diffusion in cardiac tissue for delineating the fibrous and laminar structures of cardiac muscle [1,24,25,26] and for the remodeling that occurs after heart diseases [27,28,29]. Some experiments have been done on the in-vivo heart using some approximations and configurations of the motion of the heart [30,31,32,33], however the problem of correlation between the results and real data is still an open problem, even for the case of static organs [22]. Knowing the mathematical behavior of the signal in a deforming media might help to interpret results obtained on the living heart. Simulations could then be performed to determine what parameters could be optimized to have a more accurate simulation of the DTMRI acquisition of the in-vivo cardiac system.
After presenting the mathematical context of the diffusion process, there will be a review of the method of diffusion acquisition in the static and dynamic case. Then the equation defining the behavior of the MRI signal in the context of a deforming media will be introduced, an application will be provided in the case of the prolate spheroidal coordinates [34,35], and the method of the numerical solution of this equation will be developed.
When looking at the microscopic resolution, fluid molecules are in constant motion because of thermal agitation. This random motion was initially noticed by the Scottish naturalist Robert Brown in 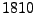 when he recorded the oscillatory motion of pollen grains suspended in water. This observation remained a mystery until Albert Einstein's kinetic-molecular theory was established in
when he recorded the oscillatory motion of pollen grains suspended in water. This observation remained a mystery until Albert Einstein's kinetic-molecular theory was established in 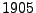 . It stated that each molecule is agitated due to thermodynamic effects and each follows a random path. At a macroscopic resolution, each small region of water diffuses around its initial position. This diffusion can occur from one substance into another but it can also occur from one region of water to another region of water.
To relate the microscopic resolution to the macroscopic resolution, Einstein introduced the diffusion coefficient
. It stated that each molecule is agitated due to thermodynamic effects and each follows a random path. At a macroscopic resolution, each small region of water diffuses around its initial position. This diffusion can occur from one substance into another but it can also occur from one region of water to another region of water.
To relate the microscopic resolution to the macroscopic resolution, Einstein introduced the diffusion coefficient 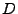 such that in the one dimensional case
such that in the one dimensional case
![$\displaystyle 6\tau\,D=\left[x\left(t+\tau\right)-x\left(t\right)\right]^2$](img5.png) , , |
|
where the molecule of water is positioned at the position 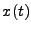 at the time
at the time 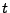 and moves to the position
and moves to the position 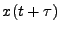 at the time
at the time  due to diffusion.
In the case of three dimensional displacement for many molecules, the relative displacement of a molecule at a position
due to diffusion.
In the case of three dimensional displacement for many molecules, the relative displacement of a molecule at a position 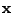 (where bold letter refers to vectors) is designated by the vector
(where bold letter refers to vectors) is designated by the vector
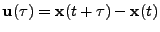 , which is a function of time
, which is a function of time 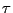 . The diffusion coefficient is therefore expressed as the dot product:
. The diffusion coefficient is therefore expressed as the dot product:
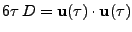 . . |
|
The characteristic length 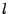 is then introduced such that
is then introduced such that
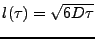 . This length is characteristic of the expansion taken by any small section of water during a time
. This length is characteristic of the expansion taken by any small section of water during a time 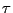 when diffusion occurs. If some molecules of water initially positioned at the origin are followed during a time
when diffusion occurs. If some molecules of water initially positioned at the origin are followed during a time 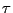 , they will spread homogeneously around a circle of radius
, they will spread homogeneously around a circle of radius 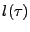 .
.
Thus far, the diffusive media has been considered to be isotropic, meaning that diffusion proprieties are identical in all directions, which is true for fluids. In biological tissues (such as fibrous tissues) [36,37], polymers [38] or nematic liquid crystals (where all the molecules point in the same direction but do not share the same row formation) [39], material microstructures are aligned along some directions. This alignment enables the molecule of water to move more easily in the direction of the alignment than in the perpendicular one [22]. This diffusion differs from the ``intrinsic'' diffusion in that it depends on the interaction of the molecule of water with the physical structure of the material. This type of diffusion should therefore be called ``apparent'' diffusion or ``restricted'' diffusion and measures only the mobility of the molecule of water in the given physical structure (cellular structure in the case of the biological sample). The given coefficient
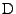 should therefore be called ``Apparent'' Diffusion Coefficient (ADC). However, the two terms are usually mixed to simplify the expression.
In anisotropic diffusion, this diffusion depends on the orientation and an initial region of water will not spread as a spherical shape. Taking the hypothesis of a simple model where only one direction is promoted at each position, the diffusion tensor can be introduced by using the notation:
should therefore be called ``Apparent'' Diffusion Coefficient (ADC). However, the two terms are usually mixed to simplify the expression.
In anisotropic diffusion, this diffusion depends on the orientation and an initial region of water will not spread as a spherical shape. Taking the hypothesis of a simple model where only one direction is promoted at each position, the diffusion tensor can be introduced by using the notation:
 , , |
(1) |
where 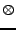 represents the tensorial product. This coefficient
represents the tensorial product. This coefficient
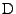 is therefore a tensor of rank two and is represented by a symetric
is therefore a tensor of rank two and is represented by a symetric 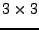 positive definite matrix by its definition in Eq. 1. This matrix depends unfortunately on the basis in which the acquisition has been performed1.
This matrix is build as a quadratic form and maps the unit sphere into an ellipsoid. This ellipsoid can always be separated in three main directions by eigenvalues decomposition.
The first direction is the elongated part of the ellipsoid at a distance
positive definite matrix by its definition in Eq. 1. This matrix depends unfortunately on the basis in which the acquisition has been performed1.
This matrix is build as a quadratic form and maps the unit sphere into an ellipsoid. This ellipsoid can always be separated in three main directions by eigenvalues decomposition.
The first direction is the elongated part of the ellipsoid at a distance 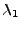 of the origin and in the direction
of the origin and in the direction 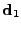 where
where 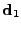 is a unitary vector. Along this direction
is a unitary vector. Along this direction 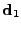 , the displacement of the molecules of water are the largest, therefore it is denoted as the Principal Direction of the apparent Diffusion (PDD). Two other directions can be differentiated using the same notation, the medium and the smallest side of the ellipsoid are then defined by the direction
, the displacement of the molecules of water are the largest, therefore it is denoted as the Principal Direction of the apparent Diffusion (PDD). Two other directions can be differentiated using the same notation, the medium and the smallest side of the ellipsoid are then defined by the direction 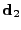 and
and  with the respective size
with the respective size 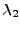 and
and 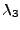 .
The diffusion tensor can therefore be decomposed in an appropriate basis where the tensor is diagonal
.
The diffusion tensor can therefore be decomposed in an appropriate basis where the tensor is diagonal
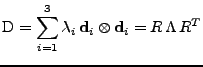 , , |
|
where 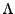 is the diagonal matrix
is the diagonal matrix
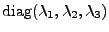 with
with
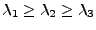 .
.
 is the rotation matrix which transforms the initial Cartesian basis into the local basis of the ellipsoid. This visualization is shown in Fig. 1
is the rotation matrix which transforms the initial Cartesian basis into the local basis of the ellipsoid. This visualization is shown in Fig. 1
Fig. 1:
Visualization of the diffusion tensor as an ellipsoid with the corresponding basis vector.
|
However, this formalism associated with the tensor of diffusion reaches some limits as soon as the material exhibits a more complex configuration. If more than one direction is promoted, as in the case of a fiber crossing in the biological tissue such as with the white matter in the brain [40], the diffusion tensor is unable to solve the problem accurately. In this case, the principal direction of diffusion will be aligned with the average of the two crossing directions leading to a large error of interpretation as illustrated in Fig. 2.
This problem is especially limiting in the case of real studies because of the partial volume effect. If large voxels are taken in account during the acquisition, the diffusion tensor has a high probability for averaging the directions that follow different paths inside this voxel. In order to have a more accurate model, higher order tensors can be used (q-ball) [41,42,43]. However, these methods still require a longer acquisition time and a strong gradient system [44] for a good signal to noise ratio (SNR). Moreover, for the purpose of the muscular fibers of the heart, the bundles are supposed to follow the same orientation in a local neighboring and therefore the direction of diffusion varies smoothly. For this reason, the tensor notation will be kept for the purpose of the current study.
Fig. 2:
Example of fiber crossing. The red tube represents an example of fiber. The blue circle shows the intersection of the fiber crossing. With the tensor approximation, the principal direction of diffusion is the average between the two directions of the fiber.
|
Performing a numerical or mathematical study of a macroscopic structure taking into account every microscopic molecule is not feasible.
The studied element, such as water, or spin orientation in the case of the MR signal, is studied as a continuous function. The macroscopic behavior is therefore known by equations that are linked to the microscopic structure via the diffusion tensor.
A scalar density of the diffusing material is introduced using the notation 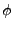 , which represents the water density or the spin orientation in one direction. This density depends on the position
, which represents the water density or the spin orientation in one direction. This density depends on the position 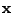 and on the time
and on the time 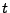 .
Denoting
.
Denoting  the density flux, Fick's first law states that this flux is given by the product of the diffusion coefficient or tensor with the spatial variation of the density (the diffusion occurs from the highest concentration to the lowest):
the density flux, Fick's first law states that this flux is given by the product of the diffusion coefficient or tensor with the spatial variation of the density (the diffusion occurs from the highest concentration to the lowest):
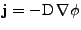 . . |
(2) |
Therefore  is a vector oriented through the local lowest concentration at each position.
The diffusion equation can be derived from the continuity equation. If no sink or sources of diffusing material exist, the time rate of change of the density equals the opposite of the divergence of the density flux:
is a vector oriented through the local lowest concentration at each position.
The diffusion equation can be derived from the continuity equation. If no sink or sources of diffusing material exist, the time rate of change of the density equals the opposite of the divergence of the density flux:
 . . |
|
And using Eq. 2 to express the flux,
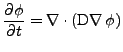 . . |
(3) |
In the case of a constant isotropic diffusion
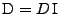 , where
, where
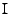 is the
is the 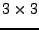 identity matrix and
identity matrix and 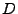 is the scalar coefficient of diffusion, Equation 3 simplifies then to the Laplace equation:
is the scalar coefficient of diffusion, Equation 3 simplifies then to the Laplace equation:
 . . |
(4) |
In the case where the boundary conditions equal zero at infinity, the solution can be expressed analytically by the convolution of the initial condition with a Gaussian function:
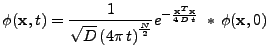 , , |
(5) |
where 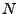 is the number of dimensions of the problem (in the space
is the number of dimensions of the problem (in the space
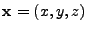 ,
,  ). The exponential function is called the Gaussian kernel of the equation and solves the problem for any initial condition given by
). The exponential function is called the Gaussian kernel of the equation and solves the problem for any initial condition given by 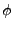 .
In the case of an anisotropic diffusion independent of time, this fundamental solution can also be expressed by [45]:
.
In the case of an anisotropic diffusion independent of time, this fundamental solution can also be expressed by [45]:
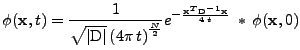 . . |
|
In the case of a vectorial diffusive density, each component of the quantity
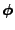 is then diffused in the material. In this case the equation of diffusion is given by the three scalar equation of diffusion:
is then diffused in the material. In this case the equation of diffusion is given by the three scalar equation of diffusion:
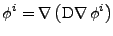 , , |
|
where
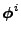 is the
is the 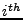 component of the vectorial quantity
component of the vectorial quantity
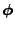 , with usually
, with usually
![$ i\in[\![1,3]\!]$](img53.png) .
To simplify the notation, the vectorial equation will be noted abusively:
.
To simplify the notation, the vectorial equation will be noted abusively:
 , , |
|
where the first operator 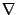 acts on the scalar quantity. To further simplify, the notation
acts on the scalar quantity. To further simplify, the notation
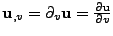 will be used:
will be used:
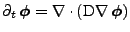 |
(6) |
The case of inhomogeneous isotropic diffusion is most often used in filtering in image processing. An example is given by taking the original noisy picture and the result given by a normal Gaussian filter comparing them to the inhomogeneous diffusion in Fig. 3. The inhomogeneous diffusion coefficient is given by
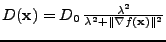 .
.
Fig. 3:
Examples of two dimensional diffusion filtering. The original image is on the top left and Gaussian noise was added to this to obtain the image on the top right. The two images at the bottom show the results of the diffusion filtering. The image on the left was obtained after an isotropic homogeneous diffusion corresponding to a convolution by a constant Gaussian kernel. The image on the right is the result of the inhomogeneous diffusion. The results were obtained numerically using the technique explained at the end of the report.
|
An example of anisotropic diffusion is also given. A scalar function is given with an initial value of zero or one. Then an inhomogeneous anisotropic diffusion is performed and shown in Fig. 4. The principal directions of the diffusion are plotted on the second picture.
Fig. 4:
The first image shows the initial scalar density function composed of values zero and one. The second image shows the result of the anisotropic diffusion. The principal direction of diffusion depends on the position and is shown in the third image (the other direction of diffusion can be neglected for being 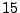 times smaller).
times smaller).
|
Diffusion Tensor Magnetic Resonance Imaging (DTMRI) provides a way to access the tissue microstructure by having knowledge of the diffusion with a large number of samples.
DTMRI is a link to the classical MRI [46].
Atoms such as
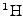 , which are especially abundant in water and therefore in biological tissue, possess a nuclear spin angular momentum. These can be visualized as spinning charged spheres that give rise to a small magnetic moment.
When a magnetic field
, which are especially abundant in water and therefore in biological tissue, possess a nuclear spin angular momentum. These can be visualized as spinning charged spheres that give rise to a small magnetic moment.
When a magnetic field 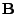 is applied to these spins, the magnetic moment vector tends to align along the direction of the field. The nuclear spins are in resonance at the pulsation called the Lamor frequency:
is applied to these spins, the magnetic moment vector tends to align along the direction of the field. The nuclear spins are in resonance at the pulsation called the Lamor frequency:
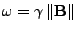 , , |
(7) |
where 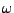 is the pulsation of the spin and
is the pulsation of the spin and 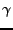 is the gyromagnetic ratio such that
is the gyromagnetic ratio such that
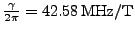 .
By convention, the
.
By convention, the 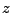 axis is aligned with the largest main magnetic field
axis is aligned with the largest main magnetic field 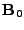 and a Cartesian basis
and a Cartesian basis
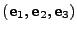 is introduced such that any vector
is introduced such that any vector
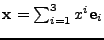 and the
and the 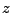 axis is aligned with the vector
axis is aligned with the vector 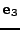 .
In order to separate the spins from the huge magnetic field
.
In order to separate the spins from the huge magnetic field 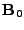 (
( T), the radiofrequency field pulse
T), the radiofrequency field pulse 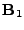 is applied at the Lamor frequency in the normal plane of
is applied at the Lamor frequency in the normal plane of 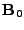 to excite the spins out of equilibrium and make them more aligned in this normal
to excite the spins out of equilibrium and make them more aligned in this normal
 plane.
In order to create a dephasing between the spins, and therefore to differentiate them, a magnetic gradient
plane.
In order to create a dephasing between the spins, and therefore to differentiate them, a magnetic gradient 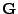 is added in the spatial direction during the reading process. Then the acquisition is performed and the spin signal coming from the component situated in the normal plane of
is added in the spatial direction during the reading process. Then the acquisition is performed and the spin signal coming from the component situated in the normal plane of 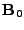 is acquired.
The magnetization vector of each spin
is acquired.
The magnetization vector of each spin 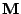 is characterized by the Bloch equation [47]:
is characterized by the Bloch equation [47]:
 , , |
|
where
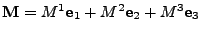 ,
,
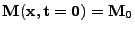 and (
and ( ,
,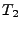 ) are the relaxation coefficients which depend on the tissue.
In this equation the total magnetic field
) are the relaxation coefficients which depend on the tissue.
In this equation the total magnetic field 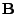 can be written as:
can be written as:
In order to take into account the diffusion process, the Bloch equation is modified into the Bloch-Torrey equation [48] by adding the diffusion contribution given by Eq. 6 where the vectorial density is given by the magnetization vector 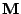 :
:
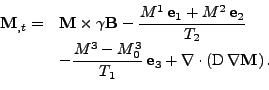 |
(8) |
The DTMRI measurement is performed for the component of the magnetization transverse to the 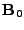 field. Then only the
field. Then only the 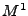 and
and  components are of interest for the signal acquisition. The complex notation is used where
components are of interest for the signal acquisition. The complex notation is used where
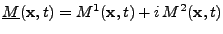 . Equation 8 is rewritten as:
. Equation 8 is rewritten as:
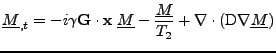 . . |
(9) |
In order to find an analytical solution, it is supposed that for a given position of the molecule, the diffusion tensor
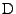 does not vary with the displacement of the molecule due to the diffusion. It is also supposed that this tensor does not depend on
does not vary with the displacement of the molecule due to the diffusion. It is also supposed that this tensor does not depend on 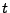 . Then, for every position
. Then, for every position 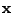 , the tensor
, the tensor
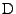 is constant.
The attenuation expresses the loss of acquired signal caused by the diffusion. In some conditions, this attenuation can be analytically expressed. The complex magnetization is therefore separated as attenuation caused by the diffusion
is constant.
The attenuation expresses the loss of acquired signal caused by the diffusion. In some conditions, this attenuation can be analytically expressed. The complex magnetization is therefore separated as attenuation caused by the diffusion  , exponential decreasing of intensity of characteristic time
, exponential decreasing of intensity of characteristic time
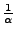 because of the relaxation parameter
because of the relaxation parameter 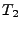 , and a phase component given by the spin phase
, and a phase component given by the spin phase  .
The general expression of the complex magnetization vector is therefore given by:
.
The general expression of the complex magnetization vector is therefore given by:
 , , |
(10) |
where the expression 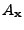 indicates that this attenuation is given for a fixed position as an argument and not as a variable.
Plugging this substitution into Eq. 9 gives the expression:
indicates that this attenuation is given for a fixed position as an argument and not as a variable.
Plugging this substitution into Eq. 9 gives the expression:
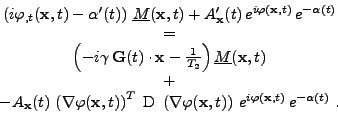 |
(11) |
The spin phase  is defined as:
is defined as:
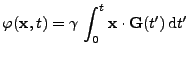 , , |
|
and the attenuation 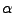 is such that :
is such that :
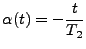 . . |
|
Equation 11 can therefore be rewritten as:
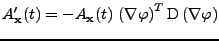 , , |
(12) |
where, in the case of the Cartesian coordinate system,
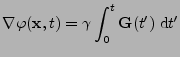 . . |
(13) |
The matrix  can be defined as the outer product
can be defined as the outer product
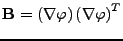 . Then Eq. 12 can be written using the trace operator
. Then Eq. 12 can be written using the trace operator
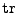 (The following equation is true in every coordinate system and will be proved in the Cartesian and curvilinear case in the following parts.):
(The following equation is true in every coordinate system and will be proved in the Cartesian and curvilinear case in the following parts.):
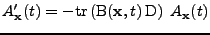 . . |
(14) |
This is a first order differential equation that can be solved analytically to give the attenuation at every position compared to the initial signal:
The DTMRI technique can access the value of the attenuation
 ; and the value of
; and the value of
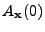 is approximated by an acquisition performed by a normal MRI technique (where the signal is supposed to be unattenuated by the diffusion).
Then the results are usually presented by the relation that links the attenuation to the diffusion tensor:
is approximated by an acquisition performed by a normal MRI technique (where the signal is supposed to be unattenuated by the diffusion).
Then the results are usually presented by the relation that links the attenuation to the diffusion tensor:
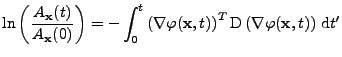 , , |
(15) |
or with the matrix  , using the linearity of the integral and the fact that
, using the linearity of the integral and the fact that
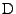 is considered as a constant through time
is considered as a constant through time
![$\displaystyle \ln\left(\frac{A_{\bf x}(t)}{A_{\bf x}(0)}\right)
=
-
\mathrm{...
...int_{0}^{t}
\mathrm{B}({\bf x},t')
\mathrm{d}t'
\right)
\mathrm{D}
\right]$](img113.png) . . |
(16) |
In order to measure the effect caused by the diffusion in a static organ such as the brain or ex-vivo heart, a special pulse sequence is performed. This pulse sequence is usually the spin echo diffusion sequence introduced by Stejskal and Tanner [49].
After the classical RF pulse, which flips the magnetization vector at
 [46], a constant gradient of diffusion
[46], a constant gradient of diffusion 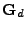 is applied during a time
is applied during a time  . During this time, the water molecules are dephased depending on their positions.
At time
. During this time, the water molecules are dephased depending on their positions.
At time
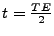 after the RF pulse, a
after the RF pulse, a
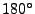 pulse is applied to invert the phase of the spins. Then a second gradient
pulse is applied to invert the phase of the spins. Then a second gradient 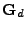 is applied during the same period of time
is applied during the same period of time  . This is the rephasing part. If the molecule is fixed, the spin will be exactly rephased at the end of this second gradient of diffusion. However, if the molecule has moved because of the diffusion in the direction of the gradient, then the phase will not be exactly recovered.
At the time
. This is the rephasing part. If the molecule is fixed, the spin will be exactly rephased at the end of this second gradient of diffusion. However, if the molecule has moved because of the diffusion in the direction of the gradient, then the phase will not be exactly recovered.
At the time 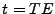 , after the initial RF pulse, and because of the phase inversion, a spin echo occurs and the MRI acquisition is performed. The sequence of the pulse is drawn in Fig. 5.
, after the initial RF pulse, and because of the phase inversion, a spin echo occurs and the MRI acquisition is performed. The sequence of the pulse is drawn in Fig. 5.
Fig. 5:
The classical spin-echo diffusion weighted sequence. The magnetization vector is flipped by the RF pulse, then the diffusion gradient 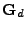 is applied during the time
is applied during the time  . After a time
. After a time
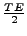 , the magnetization vector is inverted and a second gradient diffusion is applied during the same amount of time. After a time
, the magnetization vector is inverted and a second gradient diffusion is applied during the same amount of time. After a time  , the spin echo occurs and the signal is acquired using the reading gradients.
, the spin echo occurs and the signal is acquired using the reading gradients.
|
The DTMRI technique reconstructs the diffusion tensor by measuring the attenuation of the received signal, whereas, a classical MRI acquisition is done without the diffusion tensor (in this case the attenuation caused by the diffusion is supposed to be negligible). Then a reconstruction process is done to determine the value of the diffusion tensor utilizing knowledge of the attenuation factor at each position.
In the case of a fixed organ defined by the Cartesian coordinates, the relation given in Eq. 13 can be used and the matrix
 is therefore expressed as:
is therefore expressed as:
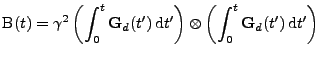 , , |
(17) |
where the integral of the gradient can be analytically expressed with knowledge of the pulse sequence. The origin of time is taken when the first gradient of diffusion begins:
 |
(18) |
The signal acquisition is performed at the time 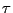 , then the matrix
, then the matrix
 is expressed by:
is expressed by:
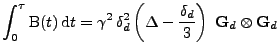 , , |
(19) |
which is proven in appendix A. The measurement of the attenuation gives the relation:
![$\displaystyle \ln\left(\frac{A_{\bf x}(t)}{A_{\bf x}(0)}\right)
=
-
\gamma^2...
...rm{tr}
\left[
\left(
{\bf G}_d\otimes{\bf G}_d
\right)
\mathrm{D}
\right]$](img127.png) , , |
(20) |
where it is proven in appendix B that
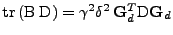 in Cartesian coordinates.
In the case where
in Cartesian coordinates.
In the case where
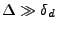 , the equation is usually simplified as:
, the equation is usually simplified as:
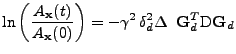 , , |
(21) |
where the time 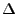 is called the effective diffusion time and the scalar
is called the effective diffusion time and the scalar
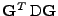 is called the effective diffusion coefficient that represents the projection of the diffusion tensor onto the direction of the gradient.
The knowledge of this projection of the tensor can be visualized by taking the length of the ellipsoid of diffusion in the direction given by the gradient. This information enables reconstruction of the diffusion tensor by recording this projection value in different directions [11,50].
Finally, denoting
is called the effective diffusion coefficient that represents the projection of the diffusion tensor onto the direction of the gradient.
The knowledge of this projection of the tensor can be visualized by taking the length of the ellipsoid of diffusion in the direction given by the gradient. This information enables reconstruction of the diffusion tensor by recording this projection value in different directions [11,50].
Finally, denoting
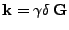 , the equation can be given in the form:
, the equation can be given in the form:
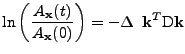 . . |
(22) |
To simplify the following notation, the Einstein summation convention is used such that for a repeated index
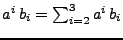 .
The curvilinear coordinates are introduced to follow the deformations of the material. The fixed Cartesian basis
.
The curvilinear coordinates are introduced to follow the deformations of the material. The fixed Cartesian basis
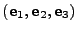 will serve as the initial frame of reference. Every position in the initial reference frame is given by the vector
will serve as the initial frame of reference. Every position in the initial reference frame is given by the vector
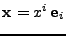 . When the material is deformed, the new position is located using curvilinear coordinates
. When the material is deformed, the new position is located using curvilinear coordinates
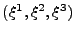 [51,35] with the contravariant basis
[51,35] with the contravariant basis
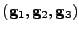 . The covariant basis will be denoted
. The covariant basis will be denoted
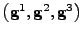 . Every position in the deformed material is given by the vector
. Every position in the deformed material is given by the vector
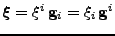 , where
, where 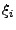 are the contravariant components of the vector.
The basis is not necessarily an orthonormal basis, and therefore
are the contravariant components of the vector.
The basis is not necessarily an orthonormal basis, and therefore
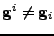 .
The curvilinear basis is given by its covariant vectors:
.
The curvilinear basis is given by its covariant vectors:
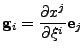 , , |
|
or its contravariant vectors:
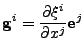 . . |
|
The arc element in the deforming material is given by
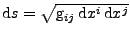 , where the contravariant metric tensor is introduced such that
, where the contravariant metric tensor is introduced such that
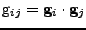 . The covariant metric tensor is defined by
. The covariant metric tensor is defined by
 and the two metric tensors are related by a matrix inversion such that
and the two metric tensors are related by a matrix inversion such that
![$ [\mathrm{g}_{ij}]=[\mathrm{g}^{ij}]^{-1}$](img149.png) , where
, where ![$ [ \;\;]$](img150.png) indicates a matrix.
indicates a matrix.
The special tensor  will be used such that
will be used such that
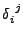 and
and
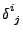 equal one if
equal one if 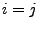 and zero otherwise.
and zero otherwise.
The tensor
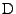 is expressed in the original coordinate system by
is expressed in the original coordinate system by
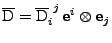 . The tensor expressed in the new coordinate system will be denoted
. The tensor expressed in the new coordinate system will be denoted
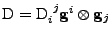 .
The diffusion tensor follows the rules of the transformation of a tensor of rank two:
.
The diffusion tensor follows the rules of the transformation of a tensor of rank two:
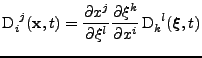 |
(23) |
It is shown in appendix C that the transformation of the tensor is given by:
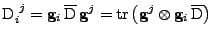 |
(24) |
The 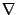 operator is given by:
operator is given by:
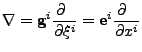 |
(25) |
The Christoffel symbols of second kind 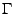 [52,53] are also defined such that:
[52,53] are also defined such that:
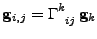 , , |
(26) |
and are related to the coordinate by the following relation:
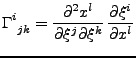 . . |
(27) |
The derivative of the covariant basis vector will also be used and it is proven in appendix D that:
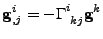 . . |
|
The Christoffel symbols can also be calculated by the relation with the metric tensor
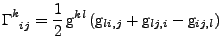 . . |
(28) |
Some relations about tensors reminded here will be used later.  ,
, 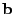 ,
, 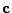 and
and 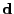 designate any vectors.
designate any vectors.
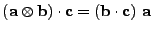 |
(29) |
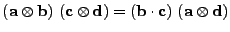 |
(30) |
The media in which the diffusion occurs is now supposed to be deformable through time.
In the following section, the implicit Einstein summation convention will be used such that
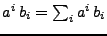 .
To study the mechanical deformation, the referential (or Lagrangian) approach is used [54,51,55].
.
To study the mechanical deformation, the referential (or Lagrangian) approach is used [54,51,55].
The fixed original referential is given by the basis
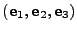 , and every initial position for this basis is given by
, and every initial position for this basis is given by
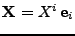 .
The material can then be deformed; the curvilinear basis associated with the deformation was introduced in the previous section. The curvilinear basis is related to the initial coordinate by the vectorial function
.
The material can then be deformed; the curvilinear basis associated with the deformation was introduced in the previous section. The curvilinear basis is related to the initial coordinate by the vectorial function
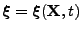 .
.
Fig. 6:
Example of deformation, where the image on the left represents the undeformed initial referential and the image on the right is the deformed referential where the curvilinear basis depends on the position.
|
The deformation is expressed with the tensorial deformation gradient such that
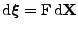 , where
, where
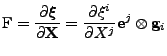 . . |
|
The measurement of the diffusion tensor in the case of the deforming heart has been performed by Reese et al. [30,31,32,33]. For this purpose, a special pulse sequence is performed.
After the RF flip angle at the time 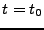 , the initial diffusion gradient is turned on during the time
, the initial diffusion gradient is turned on during the time  . After a time
. After a time
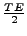 , a second RF pulse is performed, but only at
, a second RF pulse is performed, but only at
 . The cardiac cycle is trigged, and the sequence waits for the next R-wave that occurs at the time
. The cardiac cycle is trigged, and the sequence waits for the next R-wave that occurs at the time 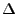 . After a time
. After a time
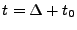 , a third RF pulse at
, a third RF pulse at
 is performed and the second diffusion gradient is applied. This diffusion gradient
is performed and the second diffusion gradient is applied. This diffusion gradient 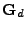 is identical to the first one and occurs during the same configuration of the heart. After the time
is identical to the first one and occurs during the same configuration of the heart. After the time
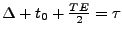 , the stimulated echo occurs and the acquisition is performed. The sequence is represented in Fig. 7
, the stimulated echo occurs and the acquisition is performed. The sequence is represented in Fig. 7
Fig. 7:
The Pulse sequence used for the dynamic acquisition. The cardiac cycle is trigged on the Electrocardiogram (ECG). After the first R-wave, an RF pulse is used to flip the magnetization to
 . The diffusion gradient
. The diffusion gradient 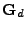 is then applied during the time
is then applied during the time  and a second RF flip is applied after the first one. The second R-wave is trigged and a third magnetization flip is applied. A second gradient of diffusion is performed (identical to the first one) and the signal acquisition is performed when the spin echo occurs at
and a second RF flip is applied after the first one. The second R-wave is trigged and a third magnetization flip is applied. A second gradient of diffusion is performed (identical to the first one) and the signal acquisition is performed when the spin echo occurs at 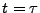 .
.
|
Equations 15 and 16 are still true (the proof in the curvilinear coordinate of Eq. 16 is exactly the same as in the Cartesian coordinates) but the spin phase is now defined in the deformed material
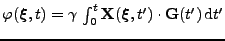 . Considering a smooth deformation, the differential relation for the spin phase is therefore:
. Considering a smooth deformation, the differential relation for the spin phase is therefore:
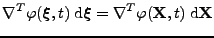 . . |
|
Using the fact that the deformation gradient is defined by
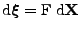 , the following relation links the gradient to the spin phase:
, the following relation links the gradient to the spin phase:
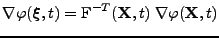 , , |
(31) |
where
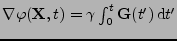 .
The tensor of diffusion is also expressed in the deformed basis, denoting
.
The tensor of diffusion is also expressed in the deformed basis, denoting
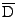 the tensor expressed in the initial referential[52]:
the tensor expressed in the initial referential[52]:
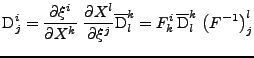 , , |
|
that can be expressed in the matrix form:
 . . |
(32) |
Denoting
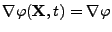 , for the sake of simplicity, the complete measured attenuation is therefore given by applying Eq. 32 and 31 to Eq. 15:
, for the sake of simplicity, the complete measured attenuation is therefore given by applying Eq. 32 and 31 to Eq. 15:
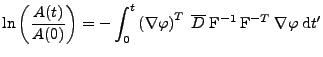 , , |
|
The deformation tensor can always be decomposed between stretch and rotation such that
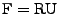 [54], where
[54], where
 is a rotation matrix such that
is a rotation matrix such that
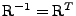 and
and
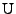 is the right stretch tensor, which is a symmetric matrix. Then the following relation holds:
is the right stretch tensor, which is a symmetric matrix. Then the following relation holds:
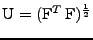 . The attenuation can therefore be decomposed such that:
. The attenuation can therefore be decomposed such that:
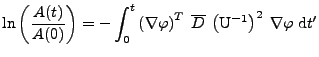 . . |
(33) |
If it is assumed that only a linear deformation affects the diffusion tensor
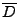 from the referential system via rotation during the time of the acquisition[56], then the cardiac deformation is assumed to be treated locally as a rigid body. The attenuation given by Eq. 15 is:
from the referential system via rotation during the time of the acquisition[56], then the cardiac deformation is assumed to be treated locally as a rigid body. The attenuation given by Eq. 15 is:
 , , |
(34) |
and using
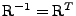 and
and
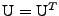
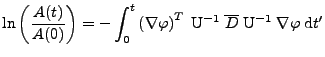 . . |
(35) |
The integral can be simplified with the knowledge of the pulse sequence used:
It is assumed that
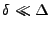 where
where 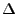 covers a complete cardiac cycle close to
covers a complete cardiac cycle close to 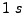 for a human and
for a human and
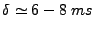 . Then the first part of the integral is negligible compared to the second part. Denoting
. Then the first part of the integral is negligible compared to the second part. Denoting
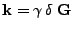 , the attenuation can therefore be approximated as:
, the attenuation can therefore be approximated as:
 |
(36) |
This equation can be rewritten in the classical form as in the static case by comparison with Eq. 22:
 |
(37) |
where the observed diffusion
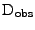 is changed due to the deformation such that:
is changed due to the deformation such that:
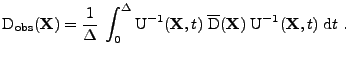 |
(38) |
Finally, the strain tensor can be introduced as defined by:
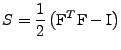 , , |
|
where
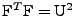 .
If the strain is small, a first order linear approximation can be used:
.
If the strain is small, a first order linear approximation can be used:
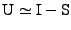 . . |
|
Then, the first order approximation of the observed diffusion is given by:
 |
(39) |
In order to enable the simulation of the MR signal in a deforming media, the Bloch-Torrey equation is expressed in curvilinear coordinates that have been introduced in the previous section.
In Cartesian coordinates, using the notation of Eq. 8, the three dimensional set of equations is given by:
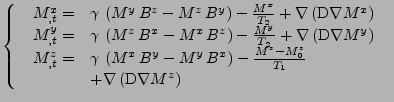 |
(40) |
where 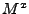 ,
, 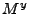 , and
, and 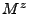 depend on the Cartesian components
depend on the Cartesian components 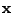 .
The part that depends on the coordinate system is the diffusive part. A general scalar
.
The part that depends on the coordinate system is the diffusive part. A general scalar 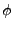 is introduced to express any component of the magnetization vector. The expression
is introduced to express any component of the magnetization vector. The expression
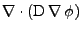 is then expressed in the new coordinate system.
In the case of the Cartesian coordinates, it is shown in appendix E, that the diffusion part can be expressed as:
is then expressed in the new coordinate system.
In the case of the Cartesian coordinates, it is shown in appendix E, that the diffusion part can be expressed as:
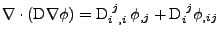 . . |
(41) |
This equation can be inserted in Eq. 40 where 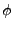 is respectively replaced by
is respectively replaced by 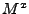 ,
, 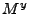 , and
, and 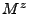 in the three scalar equations.
in the three scalar equations.
The curvilinear coordinates designated by the vector
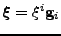 are used. The tensor
are used. The tensor
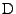 is expressed in the new coordinate system by the relation given in Eq. 24.
The density flux
is expressed in the new coordinate system by the relation given in Eq. 24.
The density flux
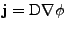 can be expressed as in the case of the Cartesian coordinates (see beginning of appendix F).
can be expressed as in the case of the Cartesian coordinates (see beginning of appendix F).
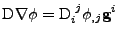 , , |
(42) |
where 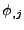 denotes
denotes
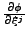 .
Finally, the diffusion is given by the divergence of this flux and gives the expression proven in appendix F:
.
Finally, the diffusion is given by the divergence of this flux and gives the expression proven in appendix F:
![$\displaystyle \nabla\cdot\left(\mathrm{D}\nabla\phi\right)
=
\left[
\left(\t...
...{\Gamma}{^l_{ji}}\tensor{\mathrm{D}}{_l^k}\,\phi_{,k}
\right]
\mathrm{g}^{ij}$](img229.png) . . |
(43) |
The complete Bloch-Torrey equation where the magnetization components are expressed on the general curvilinear coordinates is therefore given by the vectorial equation:
![\begin{displaymath}\begin{array}{*{2}{l}}
\displaystyle
{\bf M}_{,t}=&
\displ...
...\bf M}_{,k}
\right]
\,\mathrm{g}^{ij}
\mbox{ ,}
\end{array}\end{displaymath}](img230.png) |
(44) |
where 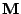 is expressed as
is expressed as
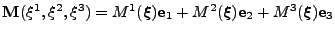 .
.
The prolate spheroidal coordinates [35] are defined by the change of variable:
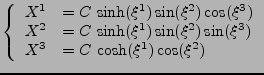 |
(45) |
The coordinates can easily model the geometry of the ventricle, as seen in fig. 8
Fig. 8:
Figure of the geometry of the prolate spheroidal coordinates.
|
The contravariant basis vectors are defined as
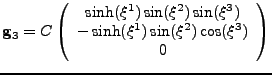 . . |
|
Then, the contravariant metric tensor is given by:
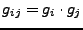 . It can be noticed that the prolate spheroidal basis is orthogonal, meaning that:
. It can be noticed that the prolate spheroidal basis is orthogonal, meaning that:
![$\displaystyle \forall (i,j)\in[\![1;3]\!]\;\;,\;i\neq j\Rightarrow {\bf g}_i\cdot {\bf g}_j=0$](img238.png) . . |
|
Therefore, only the diagonal entries of the metric tensor are not zero:
The covariant metric tensor is obtained by inverting the matrix of the contravariant metric tensor. Since it is diagonal, the inversion is obvious:
In this case of orthogonal coordinates, the scalar factors 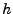 are defined such that
are defined such that
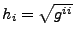 (no summation convention). Then the change of volume in the new coordinate system is given by:
(no summation convention). Then the change of volume in the new coordinate system is given by:
The covariant basis vectors given by
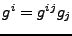 are easily calculated in the orthogonal case by
are easily calculated in the orthogonal case by
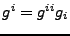 (no summation convention).
Finally, the Christoffel symbols are expressed using Eq. 28. The non zero components are given by:
(no summation convention).
Finally, the Christoffel symbols are expressed using Eq. 28. The non zero components are given by:
 |
(46) |
where
Finally, the equation can be rewritten taking into account that the metric tensor is diagonal. Writing the summation symbols, the equation for an orthogonal curvilinear system of Eq. 44 is therefore:
![\begin{displaymath}\begin{array}{*{2}{l}}
{\bf M}_{,t}=
&
\displaystyle
{\bf...
...{,k}
\right)
\Bigr)
\biggr]
\Biggr)
\mbox{ .}
\end{array}\end{displaymath}](img249.png) |
(47) |
The one-dimensional scalar equation with constant diffusion coefficient in the Cartesian case is given in Eq. 4.
In order to use the finite differences methods, the numerical differentiation operator
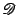 is introduced [57,58]:
is introduced [57,58]:
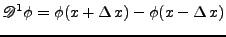 , , |
|
where 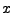 is the one dimensional variable.
This operator is the central difference operator and is second order accurate provided that
is the one dimensional variable.
This operator is the central difference operator and is second order accurate provided that
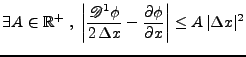 . . |
|
The second derivative in space is also a second order centered scheme:
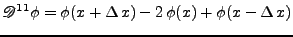 , , |
|
where
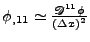 .
The temporal derivative is approximated by the first order forward scheme [59]:
.
The temporal derivative is approximated by the first order forward scheme [59]:
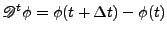 . . |
(48) |
The function is discretized on a spatial grid of intervals of size 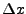 . Every position
. Every position
 is denoted to simplify by
is denoted to simplify by 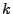 . The grid is divided in
. The grid is divided in 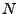 intervals where the index starts at zero. The function is stored as a vector
intervals where the index starts at zero. The function is stored as a vector 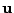 such that
such that
![$ \phi(k\Delta x)=u[k]$](img261.png) .
The matrix operator that acts on the vector directly is introduced by using the same notation. The matrix
.
The matrix operator that acts on the vector directly is introduced by using the same notation. The matrix
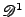 is for instance described by:
is for instance described by:
and
Both can be easily computed by using the convolution mask such that
![$ \mathscr{D}^1=\mathrm{I}_{N}\ast[-1,0,1]$](img265.png) ,
,
![$ \mathscr{D}^{11}=\mathrm{I}_N\ast[1,-2,1]$](img266.png) where
where
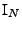 is the identity matrix of size
is the identity matrix of size 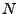 , and the result of the convolution is cropped to the size
, and the result of the convolution is cropped to the size 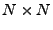 .
Therefore, the matrix product
.
Therefore, the matrix product
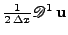 is an approximation of
is an approximation of  , respectively for
, respectively for
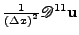 and
and
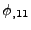 .
.
The one dimensional scalar diffusion equation given by:
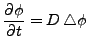 , , |
|
is rewritten in matrix form as:
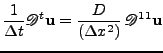 . . |
(49) |
To differentiate the unknown vector at the time
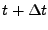 and the previously known value at the time
and the previously known value at the time 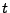 , the vector
, the vector
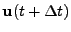 is denoted
is denoted
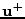 .
Then the first scheme possible to solve this equation is the first explicit Euler method, which states that:
.
Then the first scheme possible to solve this equation is the first explicit Euler method, which states that:
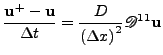 , , |
|
and gives the numerical implementable recursive algorithm:
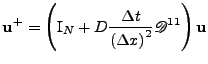 , , |
|
where knowledge of the initial condition
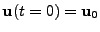 enables the calculation of the function through time. This explicit method is easily implemented, however it can be shown [58,60,61] that it is only conditionally stable since the numerical solution tends to grow faster than the real solution, and can become unstable. It is shown that the ratio
enables the calculation of the function through time. This explicit method is easily implemented, however it can be shown [58,60,61] that it is only conditionally stable since the numerical solution tends to grow faster than the real solution, and can become unstable. It is shown that the ratio
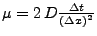 has to be such that
has to be such that 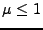 to have a stable scheme.
In this condition, the time step that can be used for the evolution decreases as the square of the number of points on the grid.
In the case of a variable diffusion coefficient in time and space, the equation of diffusion is then expressed as:
to have a stable scheme.
In this condition, the time step that can be used for the evolution decreases as the square of the number of points on the grid.
In the case of a variable diffusion coefficient in time and space, the equation of diffusion is then expressed as:
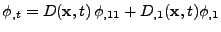 . . |
|
In this case, a stability condition also occurs on the derivative of the diffusion coefficient [58].
Calling
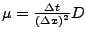 and
and
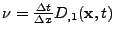 . The condition of stability is then given by:
. The condition of stability is then given by:
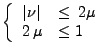 , , |
|
which implies:
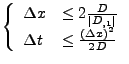 . . |
|
If the derivative of the diffusion is large compared to the gradient itself (noise in the measurement of the diffusion tensor), the spatial resolution will increase significantly and the spatial time resolution will become too small to be computed.
If this explicit method can still be applied in the one dimensional case, the two dimensional or the three dimensional cases become too complex to solve because the time step is too small and therefore requires too much computation (the condition of stability acts also on 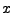 ,
,  , and
, and 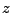 ). A numerical example is shown in Fig 9.
). A numerical example is shown in Fig 9.
Fig. 9:
Example of comparison between explicit and implicit method for the diffusion in one dimension. The picture of the left represents an initial condition of 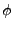 represented by a step function (slice selection of the magnetization). For the study,
represented by a step function (slice selection of the magnetization). For the study, 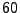 numerical sampled are taken in account for
numerical sampled are taken in account for
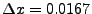 and
and
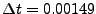 . The diffusion coefficient is constant set to
. The diffusion coefficient is constant set to 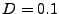 . The picture of the right shows the results after 10 iterations. The red dots represents the numerical values obtained by the implicit method, the blue cross are obtained by the explicit method. The black dotted line represents the true solution obtained by Eq. 5.
. The picture of the right shows the results after 10 iterations. The red dots represents the numerical values obtained by the implicit method, the blue cross are obtained by the explicit method. The black dotted line represents the true solution obtained by Eq. 5.
|
Another method of solving this equation is given by the first order implicit Euler method [59], coming back to Eq. 49; this method is given by:
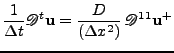 , , |
|
and give the following scheme:
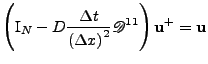 , , |
|
which can be seen as a matrix equation
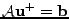 , where
, where
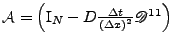 and
and
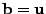 . Then the solution at the following time step is given by the solution of the linear system
. Then the solution at the following time step is given by the solution of the linear system
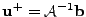 .
This complete implicit method is unconditionally stable and gives good results for the diffusion effect. Contrary to the explicit case, a slight decrease of the numerical solution occurs during the iterative process, then the numerical solution of a constant function decreases to zero. This is characteristic of a numerical diffusive effect added by this numerical method. This numerical diffusion doesn't cause a problem when the solution is supposed to be diffused; however, for the case of the Bloch-Torrey equation, the rotational term given by vectorial product needs to be solved without artificial decrease. Without diffusion, the magnitude of the solution should remain constant.
In order to get a more accurate method, the Crank-Nichols scheme was used. This method states that [58,60]:
.
This complete implicit method is unconditionally stable and gives good results for the diffusion effect. Contrary to the explicit case, a slight decrease of the numerical solution occurs during the iterative process, then the numerical solution of a constant function decreases to zero. This is characteristic of a numerical diffusive effect added by this numerical method. This numerical diffusion doesn't cause a problem when the solution is supposed to be diffused; however, for the case of the Bloch-Torrey equation, the rotational term given by vectorial product needs to be solved without artificial decrease. Without diffusion, the magnitude of the solution should remain constant.
In order to get a more accurate method, the Crank-Nichols scheme was used. This method states that [58,60]:
 , , |
|
giving the linear system:
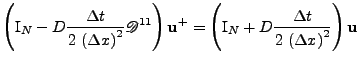 , , |
|
which can still be written as a matrix system:
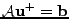 , where
, where
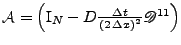 , and
, and
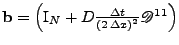 u. Due to its symmetry, this method enables the problem to be solved without artificial decrease or increase of magnitude when the real solution has a constant magnitude.
u. Due to its symmetry, this method enables the problem to be solved without artificial decrease or increase of magnitude when the real solution has a constant magnitude.
In order to apply the method to the Bloch-Torrey equation, the matrix operators of finite differences have to be defined to act on the three dimensional vector.
Now the first order center difference is given by:
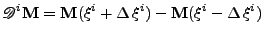 , , |
|
where  depends on
depends on
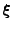 , but only the parameter on which the operator acts is reminded. The order is then given by the relation:
, but only the parameter on which the operator acts is reminded. The order is then given by the relation:
 . . |
|
The double second derivative is still given by:
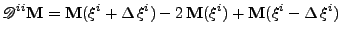 , , |
|
but the mixed derivative also needs to be defined:
where 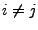 if the boundary condition is given such that
if the boundary condition is given such that  is zero outside of the area covered by the limits of the discretization.
The function
is zero outside of the area covered by the limits of the discretization.
The function 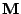 is also discretized on a grid of size
is also discretized on a grid of size
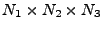 where each voxel has a volume given by
where each voxel has a volume given by
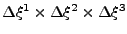 .
The function
.
The function 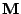 is stored on a large vector
is stored on a large vector 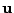 of size
of size
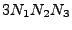 such that:
such that:
The mixed derivative matrix operator is a large square matrix of size
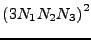 . Each line
. Each line  and column
and column  of this matrix refers to the parameters
of this matrix refers to the parameters
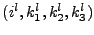 and
and
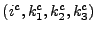 for the lines and columns respectively. The matrices are sparse and
for the lines and columns respectively. The matrices are sparse and
 is, for instance, given by:
is, for instance, given by:
![\begin{displaymath}\begin{array}{l}
[\mathscr{D}^{12}]_{I,J}=
\\
\left\{
\b...
...\\
0
&
\mbox{ otherwise}
\end{array}
\right.
\end{array}\end{displaymath}](img322.png) |
(50) |
In order to express the system with matrix operators, the matrix
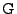 is constructed such that
is constructed such that
 corresponds to
corresponds to
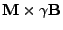 :
:
![\begin{displaymath}\begin{array}{l}
[\mathrm{G}]_{I,J}=
\\
\left\{
\begin{a...
...\\
0 & & \mbox{ otherwise}
\end{array}
\right.
\end{array}\end{displaymath}](img326.png) |
(51) |
The projection matrices on the  axis are also defined to take into account the parameters
axis are also defined to take into account the parameters  and
and 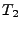 .
.
 ,
,
 , and
, and
 define the projection matrices onto
define the projection matrices onto 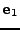 ,
, 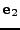 , and
, and 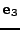 , respectively.
The matrices are defined as:
, respectively.
The matrices are defined as:
![\begin{displaymath}\begin{array}{l}
[\mathrm{P}^m]_{I,J}=
\\
\left\{
\begin...
...\\
0 & & \mbox{ otherwise}
\end{array}
\right.
\end{array}\end{displaymath}](img333.png) |
(52) |
The complete system can then be expressed as:
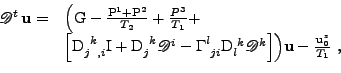 |
(53) |
where
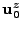 is the vector that corresponds to
is the vector that corresponds to
 and the matrix identity
and the matrix identity
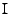 is introduced to respect the dimensions of the matrices for the addition and substraction. The equation is written in matrix form as:
is introduced to respect the dimensions of the matrices for the addition and substraction. The equation is written in matrix form as:
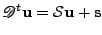 , , |
(54) |
where:
and
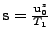 .
The equation is parabolic, therefore, the semi implicit Crank-Nicholson method introduced in the previous section is used such that:
.
The equation is parabolic, therefore, the semi implicit Crank-Nicholson method introduced in the previous section is used such that:
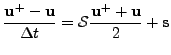 . . |
(55) |
Reorganizing the terms, the expression is given by the linear system:
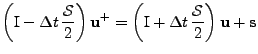 , , |
(56) |
which is a matrix system of type
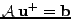 , where the matrix has dimension
, where the matrix has dimension
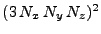 with:
with:
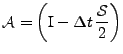 , , |
|
and
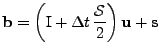 . . |
|
An overview of the diffusion process and the current methods of measurement by DTMRI have been presented concerning the static and dynamic case. The dynamic method is still being researched and the results need to be correlated and repeated by other measurements.
In order to understand the behavior of the MR signal on a deforming media such as the heart, the equation has been transformed into general curvilinear coordinate system that can fit to the geometry and deformation of the cardiac system. An example of geometrical fitting was given with the application of the prolate spheroidal system. Motion can be introduced first by expanding these coordinate by evolving the value of 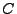 as a parameter of the coordinate system through time.
The equation expanded in the new coordinate system is linear and the diffusion part makes this equation parabolic.
as a parameter of the coordinate system through time.
The equation expanded in the new coordinate system is linear and the diffusion part makes this equation parabolic.
The numerical implementation of the solution of a diffusion equation has been presented and the importance of the implicit solution, especially for the multidimensional solution, has been iterated.
The system of equations were discretized and transformed in a linear matrix system. The solution is given by iterations following the Crank-Nicholson scheme. The rapidity of the results are however largely dependent on the size of the matrix. These matrices are very large and sparse. Different methods to solve the system have to be tested as the direct matrix inversion requires 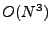 calculations [61] where
calculations [61] where 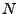 is the size of the matrix, which is given by
is the size of the matrix, which is given by
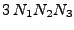 and where each
and where each 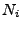 gives the size in each dimension
gives the size in each dimension  ,
,  , and
, and 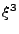 . Least squares and conjugate gradient methods enable the process to be sped up; however, for large systems where
. Least squares and conjugate gradient methods enable the process to be sped up; however, for large systems where
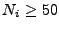 , the iteration process becomes very slow.
More research on implementing an Alternative Direction Implicit (ADI) scheme should be performed. Then each iteration should follow three passes but the matrix on the left hand side of the equation becomes tridiagonal and could be rapidly inverted using the Thomas algorithm [58,60].
, the iteration process becomes very slow.
More research on implementing an Alternative Direction Implicit (ADI) scheme should be performed. Then each iteration should follow three passes but the matrix on the left hand side of the equation becomes tridiagonal and could be rapidly inverted using the Thomas algorithm [58,60].
This work was supported in part by the Director, Office of Science, Office of Biological and Environmental Research, Medical Science Division of the U.S. Department of Energy (DEO) under Contract No. DE-AC02-05CH11231 and in part by Public Health Service (NIH) grant number R01 EB000121 awarded by the National Institute of Biomedical Imaging and Bioengineering, Department of Health and Human Services.
Proof of Eq. 19
This proof shows that with the expression of the gradient given in Eq. 18, the integral
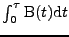 at the time of the acquisition, is given by Eq 19 where the tensor
at the time of the acquisition, is given by Eq 19 where the tensor
 is given by:
is given by:
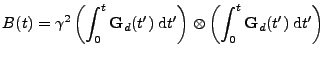 . . |
|
Using the linearity of the integral:
Introducing Eq. 18 in the expression gives:
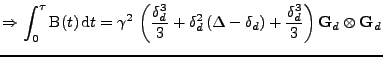 . . |
|
This giving the expected result:
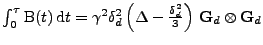 .
.
Proof of Eq. 14
The proof of Eq. 14 in the case of fixed Cartesian coordinates show that:
with
 . . |
|
It is also known that in this case of fixed organs,
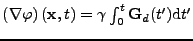 .
To simplify the notation the vector
.
To simplify the notation the vector 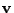 is introduced such that
is introduced such that
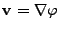 .
Then
.
Then
 and
and
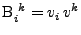 . The matrix product gives
. The matrix product gives
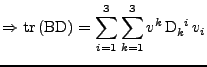 . . |
|
And on the other hand, the matrix product:
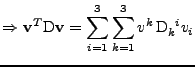 . . |
|
The two expressions are then equal, and using the fact that:
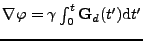 , it follows that
, it follows that
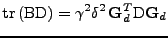 . . |
|
Proof of Eq. 24
It is shown that the transformation of the tensor of diffusion follows the rule given by Eq. 24:
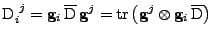 . . |
|
The first equality is developped to give:
 . . |
|
Using the relation from Eq. 29,
 , , |
|
which corresponds to the relation given in Eq. 23.
The second equality is then studied:
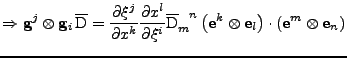 . . |
|
Using the relation on the tensorial product given in Eq. 30, the equation is simplified to:
 . . |
|
The following property of the trace operator is also used
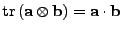 to have finally the expression of the tensor:
to have finally the expression of the tensor:
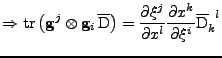 , , |
|
which is also the relation of the tensor given in Eq. 23
Proof of Eq. 26
It is proven in this appendix that
 .
Using the relation
.
Using the relation
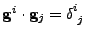 given by derivation
given by derivation
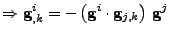 . . |
|
The Christoffel symbol is introduced with the relation of Eq 26.
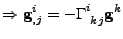 , , |
|
which ends the proof.
Proof of Eq. 41
It is shown that when the differentiation is performed on a Cartesian grid:
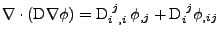 , , |
|
where
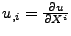 and
and 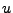 can represent
can represent
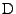 or
or 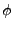 .
.
Since the Cartesian coordinate system of basis
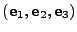 is orthonormal, the contravariant and covariant vectors are equal meaning
is orthonormal, the contravariant and covariant vectors are equal meaning
 .
Moreover, this basis doesn't depend on the position
.
Moreover, this basis doesn't depend on the position  , therefore:
, therefore:
![$\displaystyle \forall (i,j)\in[\![0;3]\!]\;\;,\;
{\bf e}_{i,j}={\bf e}^{i}_{,j}={\bf0}$](img400.png) . . |
|
The first part
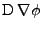 can be expressed as:
can be expressed as:
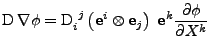 . . |
|
The relation given by Eq. 29 can then be recognized. Therefore
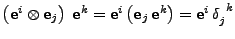 , where
, where
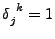 only if
only if 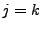 and equals 0
otherwise. Then the first part of the diffusion is given by:
and equals 0
otherwise. Then the first part of the diffusion is given by:
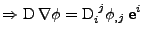 . . |
|
The complete diffusion equation is obtained by taking the divergence of this expression:
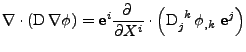 . . |
|
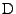 and
and 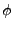 depend on the coordinates but
depend on the coordinates but 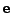 doesn't.
doesn't.
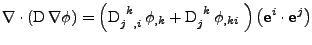 . . |
|
Assuming the scalar 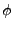 , and therefore that each component of the magnetization vector
, and therefore that each component of the magnetization vector 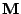 are differentiable twice to enable the Schwarz's theorem on the mixed derivative to hold [62] such that
are differentiable twice to enable the Schwarz's theorem on the mixed derivative to hold [62] such that
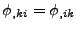 , the diffusion process is given by:
, the diffusion process is given by:
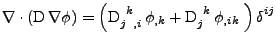 , , |
|
where, in Cartesian coordinates,
 equals one only if
equals one only if 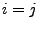 and 0
otherwise. The diffusion is therefore given by the relation of Eq. 41:
and 0
otherwise. The diffusion is therefore given by the relation of Eq. 41:
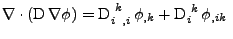 . . |
|
Proof of Eq. 43
It is proven that in curvilinear coordinates
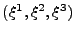 with covariant basis vectors
with covariant basis vectors
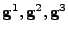 , contravariant basis vectors
, contravariant basis vectors
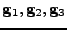 , and contravariant metric tensor
, and contravariant metric tensor
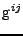 , the expression of the diffusion is given by:
, the expression of the diffusion is given by:
![$\displaystyle \nabla\cdot\left(\mathrm{D}\,\nabla\phi\right)
=
\left[
\left(...
...{\Gamma}{^l_{ji}}\tensor{\mathrm{D}}{_l^k}\,\phi_{,k}
\right]
\mathrm{g}^{ij}$](img418.png) , , |
|
where
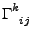 is the Christoffel symbol of second kind.
The first part of the equality
is the Christoffel symbol of second kind.
The first part of the equality
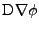 follows the same proof as for the Cartesian case:
follows the same proof as for the Cartesian case:
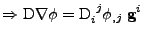 . . |
|
which corresponds to the expression given in Eq. 42.
The next part of the derivation takes the divergence of this vector such that:
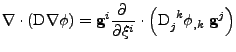 . . |
|
The derivative is expanded on the product where the vector  depends on the variable
depends on the variable  :
:
![$\displaystyle \nabla\cdot\left(\mathrm{D}\nabla\phi\right)
=
{\bf g}^i
\left...
...{,i}\;{\bf g}^j
+
\tensor{\mathrm{D}}{_j^k}\phi_{,k}\;{\bf g}^j_{,i}
\right]$](img426.png) . . |
|
The derivative of the covariant basis vector given in Eq. 4.2.1 is inserted into the relation:
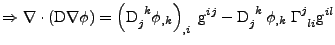 , , |
|
where the indexes  and
and  can be inverted in the last part of the sum:
can be inverted in the last part of the sum:
![$\displaystyle \Rightarrow
\nabla\cdot\left(\mathrm{D}\nabla\phi\right)
=
\le...
...{\Gamma}{^l_{ji}}\tensor{\mathrm{D}}{_l^k}\,\phi_{,k}
\right]
\mathrm{g}^{ij}$](img430.png) , , |
|
which ends the proof.
Finally, the expression can also be seen in its expanded form:
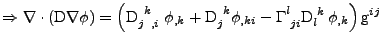 . . |
|
- 1
-
Patrick Helm, Mirza Faisal Beg, Michael I.Miller, and Raimond L.Winslow.
Measuring and mapping cardiac fiber and laminar architecture using
diffusion tensor MR imaging.
Annals of the New York Academy of Sciences,
1047:296-307, June 2005.
- 2
-
E. W. Hsu, A. L. Muzikant, S. A. Matulevicius, R. C. Penland, and C. S.
Henriquez.
Magnetic resonance myocardial fiber-orientation mapping with direct
histological correlation.
American Journal of Physiology. Heart and Circulatory
Physiology, 274(5):1627-1634, May 1998.
- 3
-
Alex Holmes.
Development of Diffusion Tensor Magnetic Resonance
Imaging Techniques for Rapid Determination of Myocardial Fiber
Orientation.
PhD thesis, Johns Hopkins University, Baltimore, Maryland,
1999.
- 4
-
Yi Jiang, Kumar Pandya, Oliver Smithies, and Edward W. Hsu.
Three-dimensional diffusion tensor microscopy of fixed mouse hearts.
Magnetic Resonance in Medicine, 52(3):453-460,
September 2004.
- 5
-
David Scollan.
Reconstructing the Heart: Development and Application of
Biophysically-Based Electrical Models of Propagation in
Ventricular Myocardium Reconstructed from Diffusion Tensor MRI.
PhD thesis, Johns Hopkins University, Baltimore, Maryland,
2002.
- 6
-
Vitaly J. Napadow, Qun Chen, Vu Mai, Peter T. C. So, and Richard J. Gilbert.
Quantitative analysis of three-dimensional-resolved fiber
architecture in heterogeneous skeletal muscle tissue using NMR and optical
imaging methods.
Biophysical Journal, 80(6):2968-2975, June 2001.
- 7
-
J. E. Tanner.
Self diffusion of water in frog muscle.
Biophysical Journal, 28(1):107-116, October 1979.
- 8
-
G. G. Cleveland, D. C. Chang, C. F. Hazlewood, and H. E. Rorschach.
Nuclear magnetic resonance measurement of skeletal muscle. anisotropy
of the diffusion coefficient of the intracellular water.
Biophysical Journal, 16(9):1043-1053, September 1976.
- 9
-
C. C. Van Donkelaar, L. J. Kretzers, P. H. M. Bovendeerd, L. M. A. Lataster,
K. Nicolay, J. D. Janseen, and M. R. Drost.
Diffusion tensor imaging in biomechanical studies of skeletal muscle
function.
Journal of ANATOMY, 194(1):79-88, January 1999.
- 10
-
Denis Le Bihan.
Looking into the functional architecture of the brain with diffusion
MRI.
Nature Reviews. Neuroscience, 4(6):459-80, June 2003.
- 11
-
Denis Le Bihan, Jean-Francois Mangin, Cyril Poupon, Chris A. Clark, Sabina
Pappata, Nicolas Molko, and Hughes Chabriat.
Diffusion tensor imaging: Concepts and applications.
Journal of Magnetic Resonance Imaging, 13(4):534-546,
April 2001.
- 12
-
Oliver Natt and Jens Frahm.
In vivo magnetic resonance imaging: Insights into structure and
function of the central nervous system.
Measurement Science and Technology, 16:R17-R36,
February 2005.
- 13
-
Thomas L. Chenevert, James A. Brunberg, and James G. Pipe.
Anisotropic diffusion in human white matter: Demonstration with
MR techniques in vivo.
Radiology, 177(2):401-5, November 1990.
- 14
-
Richard J. Gilbert, Lee H. Magnusson, Vitaly J. Napadow, Thomas Benner, Ruopeng
Wang, and Van J. Wedeen.
Mapping complex myoarchitecture in the bovine tongue with
diffusion-spectrum magnetic resonance imaging.
Biophysical Journal, 91:1014-1022, May 2006.
- 15
-
Richard J. Gilbert and Vitaly J. Napadow.
Three-dimensional muscular architecture of the human tongue
determined in vivo with diffusion tensor magnetic resonance imaging.
Dysphagia, 20(1):1-7, 2005.
- 16
-
Van J. Wedeen, Timothy G. Reese, Vitaly J. Napadow, and Richard J. Gilbert.
Demonstration of primary and secondary muscle fiber architecture of
the bovine tongue by diffusion tensor magnetic resonance imaging.
Biophysical Journal, 80(80):1024-1028, February 2001.
- 17
-
Chad A. Holder, Raja Muthupillai, Srinivasan Mukundan, James D. Eastwood, and
Patricia A. Hudgins.
Diffusion-weighted MR imaging of the normal human spinal cord in
vivo.
American Journal of Neuroradiology, 21(10):1799-1806,
November 2000.
- 18
-
Joon W. Lee, Jae H. Kim, Heung S. Kang, Jong S. Lee, Ja-Young Choi, Jin-Sup
Yeom, Hyun-Jib Kim, and Hye Chung.
Optimization of acquisition parameters of diffusion-tensor magnetic
resonance imaging in the spinal cord.
Investigative Radiology, 41(7):553-559, July 2006.
- 19
-
Robert L. Cooper, David B. Chang, Allan C. Young, Carroll J. Martin, and Betsy
Ancker Johnson.
Restricted diffusion in biophysical systems.
Biophysical Journal, 14(3):161-177, March 1974.
- 20
-
Sverre Rosenbaum.
Evaluation of Human Stroke by MR Imaging.
PhD thesis, Faculty of Medicine, University of Copenhagen,
Denmark, August 2000.
- 21
-
Josef Pfeuffer, Wolfgang Dreher, Eva Sykova, and Dieter Leibfritz.
Water signal attenuation in diffusion-weighted 1h NMR experiments
during cerebral ischemia: Influence of intracellular restrictions,
extracellular tortuosity, and exchange.
Magnetic Resonance Imaging, 16(9):1023-1032, November
1998.
- 22
-
Christian Beaulieu.
The basis of anisotropic water diffusion in the nervous system - a
technical review.
NMR in Biomedicine, 15(7-8):435-55, November 2002.
- 23
-
Burkhard Wunsche.
The visualization and measurement of left ventricular deformation.
In Proceedings of the First Asia-Pacific
Bioinformatics Conference on Bioinformatics, pages 119-128.
Australian Computer Society, Inc., 2003.
- 24
-
Leonid Zhukov and Alan H. Barr.
Heart-muscle fiber reconstruction from diffusion tensor MRI.
IEEE , Proceedings of the 14th IEEE Visualization,
page 79, October 2003.
- 25
-
Damien Rohmer, Arkadiusz Sitek, and Grant T. Gullberg.
Reconstruction and visualization of fiber and sheet structure with
regularized tensor diffusion MRI in the human heart.
Technical Report LBNL-60277, Lawrence Berkeley National
Laboratory Report, 2006.
- 26
-
Damien Rohmer, Arkadiusz Sitek, and Grant T. Gullberg.
Fiber tracking in the entire heart.
Available at http://cfi.lbl.gov/ asitek/fibertrack
/3_fiber_tracking_entire_heart.html, 2006.
- 27
-
Patrick A. Helm, Laurent Younes, Mirza F. Beg, Daniel B. Ennis, Christophe
Leclercq, Owen P. Faris, Elliot McVeigh, David Kass, Michael I. Miller, and
Raimond L. Winslow.
Evidence of structural remodeling in the dyssynchronous failing
heart.
Circulation Research, 98(1):125-132, January 2006.
- 28
-
Joseph C. Walker, Julius M. Guccione, Yi Jiang, Peng Zhang, Arthur W. Wallace,
Edward Hsu, and Mark B. Ratcliffe.
Helical myofiber orientation after myocardial infarction and left
ventricular surgical restoration in sheep.
Journal of Thoracic and Cardiovascular Surgery,
129(2):382-390, February 2005.
- 29
-
Marc A. Pfeffer and Eugene Braunwald.
Ventricular remodeling after myocardial infarction. experimental
observations and clinical implications.
Circulation, 81(4):1161-1172, April 1990.
- 30
-
Jiangang Dou, Timothy G. Reese, Wen-Yih I. Tseng, and Van J. Wedeen.
Cardiac diffusion MRI without motion effects.
Magnetic Resonance in Medicine, 48(1):105-114, July
2002.
- 31
-
Wen-Yih I. Tseng, Timothy G. Reese, Robert M. Weisskoff, Thomas J. Brady, and
Van J. Wedeen.
Myocardial fiber shortening in humans: Initial results of MR
imaging.
Radiology, 216(1):128-139, July 2000.
- 32
-
Wen-Yih I. Tseng, Timothy G. Reese, Robert M. Weisskoff, and Van J. Wedeen.
Cardiac diffusion tensor MRI in vivo without strain correction.
Magnetic Resonance in Medicine, 42(2):393-403, July
1999.
- 33
-
Timothy G. Reese, Robert M. Weisskoff, R. Neil Smith, Bruce R. Rosen, Robert E.
Dinsmore, and Van J. Wedeen.
Imaging myocardial fiber architecture in vivo with magnetic
resonance.
Magnetic Resonance in Medicine, 34(6):786-91, December
1995.
- 34
-
Bing Feng, Alexander I. Veress, and Grant T. Gullberg.
The prolate spheroidal transform for gated SPECT.
IEEE Transaction on Nuclear Science, 48:872-875,
June 2001.
- 35
-
Wolfram Neutsch.
Coordinates.
Walter de Gruyter, 1996.
- 36
-
Pabitra N. Sen and Peter J. Basser.
A model for diffusion in white matter in the brain.
Biophysical Journal, 89(5):2927-38, November 2005.
- 37
-
Pabitra N. Sen.
Diffusion and tissue microstructure.
Journal of Physics: Condensed Matter, 16:S5213-20,
November 2004.
- 38
-
Mihail S. Iotov.
Diffusion in Amorphous Media.
PhD thesis, California Institute of Technology, Pasadena
California, September 1997.
- 39
-
S. V. Dvinskikh and I. Furo.
Anisotropic self-diffusion in the nematic phase of a thermotropic
liquid crystal by 1H-spin-echo nuclear magnetic resonance.
Journal of Chemical Physics, 115(4):1946-50, July
2001.
- 40
-
Mette R. Wiegell, Henrik B. W. Larsson, and Van J. Wedeen.
Fiber crossing in human brain depicted with diffusion tensor MR
imaging.
Radiology, 217(3):897-903, December 2000.
- 41
-
David S. Tuch, Timothy G. Reese, Mette R. Wiegell, and Van J. Wedeen.
Diffusion MRI of complex neural architecture.
Neuron, 40(5):885-895, December 2003.
- 42
-
Evren Ozarslan and Thomas H. Mareci.
Generalized diffusion tensor imaging and analytical relationships
between diffusion tensor imaging and high angular resolution diffusion
imaging.
Magnetic Resonance in Medicine, 50(5):955-965,
November 2003.
- 43
-
David Solomon Tuch.
Diffusion MRI of Complex Tissue Structure.
PhD thesis, Massachusetts Institute of Technology,
Massachusetts, USA, January 2002.
- 44
-
J. R. Basser and D. K. Jones.
Diffusion-tensor MRI: theory, experimental design and data analysis
- a technical review.
NMR in Biomedicine, 15(7-8):456-467, November 2002.
- 45
-
Bernd Jahne.
Digital Image Processing.
Springer, sixth edition, 2005.
- 46
-
Dwight G. Nishimura.
Principles of Magnetic Resonance Imaging.
Stanford University, California, 1996.
- 47
-
F. Bloch.
Nuclear induction.
Pysical Review, 70(7):460-474, October 1946.
- 48
-
H. C. Torrey.
Bloch equation with diffusion terms.
Phys Rev, 104(3):563-565, November 1956.
- 49
-
E.O. Stejskal and J.E. Tanner.
Spin diffusion measurements: Spin echoes in the presence of a
time-dependent field gradient.
The Journal of Chemical Physics, 42(1):288-292,
January 1964.
Spin Echo sequence from Stejskal and Tanner for diffusion tensor MRI.
- 50
-
Cyril Poupon.
Détection des faisceaux de fibres de la substance blanche pour
l'étude de la connectivité anatomique cérébrale.
PhD thesis, Ecole Nationale Superieure des Telecommunications
de Paris, Paris, France, 1999.
- 51
-
T. J. Chung.
Applied Continuum Mechanics.
Cambridge, 1997.
- 52
-
A. I. Borisenko and I. E. Tarapov.
Vector and Tensor Analysis. With Applications.
Dover, 1979.
- 53
-
Erwin Kreysig.
Differential Geometry.
Dover, 1991.
- 54
-
Jay D. Humphrey.
Cardiovascular Solid Mechanics. Cells, Tissues, and Organs.
Springer, 2001.
- 55
-
S. P. Timoshenko and J. N. Goodier.
Theory of Elasticity.
McGraw Hill, third edition, 1987.
- 56
-
Timothy G. Reese, Van J. Wedeen, and Robert M. Weisskoff.
Measuring diffusion in the presence of material strain.
Journal of Magnetic Resonance. Series B.,
112(3):253-258, September 1996.
- 57
-
Alfio Quarteroni and Alberto Valli.
Numerical Approximation of Partial Differential Equations.
Springer, 1997.
- 58
-
K. W. Morton and D. F. Mayers.
Numerical Solution of Partial Differential Equations.
Cambridge, 2005.
- 59
-
E. Haier, S. P. Norsett, and G. Wanner.
Solving Ordinary Differential Equations I, Nonstiff Problems.
Springer, second edition, 2000.
- 60
-
J. W. Thomas.
Numerical Partial Differential Equations. Finite Difference
Methods.
Springer, 1995.
- 61
-
Alfio Quarteroni, Riccardo Sacco, and Fausto Saleri.
Numerical Mathematics.
Springer, 1991.
- 62
-
I. N. Bronshtein, K. A. Semendyayev, G. Musiol, and H. Muehlig.
Handbook of mathematics.
Springer, fourth edition, 2003.
A Bloch-Torrey Equation for Diffusion in a Deforming Media
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html MRI_diffusion.tex -split 0
The translation was initiated by damien on 2007-03-03
Footnotes
- ... performed1
- Trace and determinant are independent of the basis.
damien
2007-03-03

![]() when he recorded the oscillatory motion of pollen grains suspended in water. This observation remained a mystery until Albert Einstein's kinetic-molecular theory was established in
when he recorded the oscillatory motion of pollen grains suspended in water. This observation remained a mystery until Albert Einstein's kinetic-molecular theory was established in ![]() . It stated that each molecule is agitated due to thermodynamic effects and each follows a random path. At a macroscopic resolution, each small region of water diffuses around its initial position. This diffusion can occur from one substance into another but it can also occur from one region of water to another region of water.
To relate the microscopic resolution to the macroscopic resolution, Einstein introduced the diffusion coefficient
. It stated that each molecule is agitated due to thermodynamic effects and each follows a random path. At a macroscopic resolution, each small region of water diffuses around its initial position. This diffusion can occur from one substance into another but it can also occur from one region of water to another region of water.
To relate the microscopic resolution to the macroscopic resolution, Einstein introduced the diffusion coefficient ![]() such that in the one dimensional case
such that in the one dimensional case
![]() should therefore be called ``Apparent'' Diffusion Coefficient (ADC). However, the two terms are usually mixed to simplify the expression.
In anisotropic diffusion, this diffusion depends on the orientation and an initial region of water will not spread as a spherical shape. Taking the hypothesis of a simple model where only one direction is promoted at each position, the diffusion tensor can be introduced by using the notation:
should therefore be called ``Apparent'' Diffusion Coefficient (ADC). However, the two terms are usually mixed to simplify the expression.
In anisotropic diffusion, this diffusion depends on the orientation and an initial region of water will not spread as a spherical shape. Taking the hypothesis of a simple model where only one direction is promoted at each position, the diffusion tensor can be introduced by using the notation:
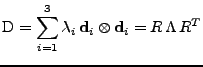 ,
,![\includegraphics[height=5.0cm]{picture/fig_fiber_cross.eps}](img33.png)
![]() , which represents the water density or the spin orientation in one direction. This density depends on the position
, which represents the water density or the spin orientation in one direction. This density depends on the position ![]() and on the time
and on the time ![]() .
Denoting
.
Denoting ![]() the density flux, Fick's first law states that this flux is given by the product of the diffusion coefficient or tensor with the spatial variation of the density (the diffusion occurs from the highest concentration to the lowest):
the density flux, Fick's first law states that this flux is given by the product of the diffusion coefficient or tensor with the spatial variation of the density (the diffusion occurs from the highest concentration to the lowest):
 .
.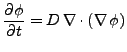
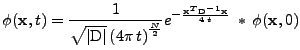 .
. ,
,![\includegraphics[height=4.0cm]{picture/fig_image_2D_original}](img59.png)
![\includegraphics[height=4.0cm]{picture/fig_image_2D_noisy}](img60.png)
![\includegraphics[height=4.0cm]{picture/fig_image_2D_isotropic}](img61.png)
![\includegraphics[height=4.0cm]{picture/fig_image_2D_anisotropic}](img62.png)
![\includegraphics[height=4.0cm]{picture/fig_diffusion_tensor_original}](img64.png)
![\includegraphics[height=4.0cm]{picture/fig_diffusion_tensor_result}](img65.png)
![\includegraphics[height=4.0cm]{picture/fig_diffusion_tensor_array}](img66.png)
![]() , which are especially abundant in water and therefore in biological tissue, possess a nuclear spin angular momentum. These can be visualized as spinning charged spheres that give rise to a small magnetic moment.
When a magnetic field
, which are especially abundant in water and therefore in biological tissue, possess a nuclear spin angular momentum. These can be visualized as spinning charged spheres that give rise to a small magnetic moment.
When a magnetic field ![]() is applied to these spins, the magnetic moment vector tends to align along the direction of the field. The nuclear spins are in resonance at the pulsation called the Lamor frequency:
is applied to these spins, the magnetic moment vector tends to align along the direction of the field. The nuclear spins are in resonance at the pulsation called the Lamor frequency:
 ,
,![]() :
:
![]() field. Then only the
field. Then only the ![]() and
and ![]() components are of interest for the signal acquisition. The complex notation is used where
components are of interest for the signal acquisition. The complex notation is used where
![]() . Equation 8 is rewritten as:
. Equation 8 is rewritten as:
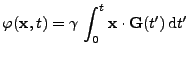 ,
,![]() [46], a constant gradient of diffusion
[46], a constant gradient of diffusion ![]() is applied during a time
is applied during a time ![]() . During this time, the water molecules are dephased depending on their positions.
At time
. During this time, the water molecules are dephased depending on their positions.
At time
![]() after the RF pulse, a
after the RF pulse, a
![]() pulse is applied to invert the phase of the spins. Then a second gradient
pulse is applied to invert the phase of the spins. Then a second gradient ![]() is applied during the same period of time
is applied during the same period of time ![]() . This is the rephasing part. If the molecule is fixed, the spin will be exactly rephased at the end of this second gradient of diffusion. However, if the molecule has moved because of the diffusion in the direction of the gradient, then the phase will not be exactly recovered.
At the time
. This is the rephasing part. If the molecule is fixed, the spin will be exactly rephased at the end of this second gradient of diffusion. However, if the molecule has moved because of the diffusion in the direction of the gradient, then the phase will not be exactly recovered.
At the time ![]() , after the initial RF pulse, and because of the phase inversion, a spin echo occurs and the MRI acquisition is performed. The sequence of the pulse is drawn in Fig. 5.
, after the initial RF pulse, and because of the phase inversion, a spin echo occurs and the MRI acquisition is performed. The sequence of the pulse is drawn in Fig. 5.
![\includegraphics[width=10.0cm]{picture/fig_pulse_sequence}](img122.png)
![]() is therefore expressed as:
is therefore expressed as:
![]() .
The curvilinear coordinates are introduced to follow the deformations of the material. The fixed Cartesian basis
.
The curvilinear coordinates are introduced to follow the deformations of the material. The fixed Cartesian basis
![]() will serve as the initial frame of reference. Every position in the initial reference frame is given by the vector
will serve as the initial frame of reference. Every position in the initial reference frame is given by the vector
![]() . When the material is deformed, the new position is located using curvilinear coordinates
. When the material is deformed, the new position is located using curvilinear coordinates
![]() [51,35] with the contravariant basis
[51,35] with the contravariant basis
![]() . The covariant basis will be denoted
. The covariant basis will be denoted
![]() . Every position in the deformed material is given by the vector
. Every position in the deformed material is given by the vector
![]() , where
, where ![]() are the contravariant components of the vector.
The basis is not necessarily an orthonormal basis, and therefore
are the contravariant components of the vector.
The basis is not necessarily an orthonormal basis, and therefore
![]() .
The curvilinear basis is given by its covariant vectors:
.
The curvilinear basis is given by its covariant vectors:
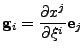 ,
,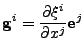 .
.![]() will be used such that
will be used such that
![]() and
and
![]() equal one if
equal one if ![]() and zero otherwise.
and zero otherwise.
![]() is expressed in the original coordinate system by
is expressed in the original coordinate system by
![]() . The tensor expressed in the new coordinate system will be denoted
. The tensor expressed in the new coordinate system will be denoted
![]() .
The diffusion tensor follows the rules of the transformation of a tensor of rank two:
.
The diffusion tensor follows the rules of the transformation of a tensor of rank two:
![]() operator is given by:
operator is given by:
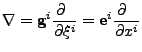
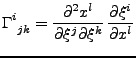 .
.![]() ,
, ![]() ,
, ![]() and
and ![]() designate any vectors.
designate any vectors.
![]() .
To study the mechanical deformation, the referential (or Lagrangian) approach is used [54,51,55].
.
To study the mechanical deformation, the referential (or Lagrangian) approach is used [54,51,55].
![]() , and every initial position for this basis is given by
, and every initial position for this basis is given by
![]() .
The material can then be deformed; the curvilinear basis associated with the deformation was introduced in the previous section. The curvilinear basis is related to the initial coordinate by the vectorial function
.
The material can then be deformed; the curvilinear basis associated with the deformation was introduced in the previous section. The curvilinear basis is related to the initial coordinate by the vectorial function
![]() .
.
![\includegraphics[height=5.0cm]{picture/fig_no_deformation.eps}](img175.png)
![\includegraphics[height=4.8cm]{picture/fig_deformation.eps}](img176.png)
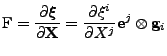 .
.![]() , the initial diffusion gradient is turned on during the time
, the initial diffusion gradient is turned on during the time ![]() . After a time
. After a time
![]() , a second RF pulse is performed, but only at
, a second RF pulse is performed, but only at
![]() . The cardiac cycle is trigged, and the sequence waits for the next R-wave that occurs at the time
. The cardiac cycle is trigged, and the sequence waits for the next R-wave that occurs at the time ![]() . After a time
. After a time
![]() , a third RF pulse at
, a third RF pulse at
![]() is performed and the second diffusion gradient is applied. This diffusion gradient
is performed and the second diffusion gradient is applied. This diffusion gradient ![]() is identical to the first one and occurs during the same configuration of the heart. After the time
is identical to the first one and occurs during the same configuration of the heart. After the time
![]() , the stimulated echo occurs and the acquisition is performed. The sequence is represented in Fig. 7
, the stimulated echo occurs and the acquisition is performed. The sequence is represented in Fig. 7
![\includegraphics[width=12.0cm]{picture/fig_pulse_sequence_dynamic}](img183.png)
![]() . Considering a smooth deformation, the differential relation for the spin phase is therefore:
. Considering a smooth deformation, the differential relation for the spin phase is therefore:
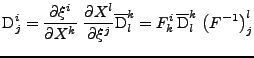 ,
,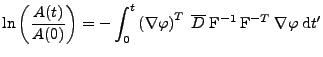 ,
,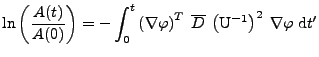 .
.![]() from the referential system via rotation during the time of the acquisition[56], then the cardiac deformation is assumed to be treated locally as a rigid body. The attenuation given by Eq. 15 is:
from the referential system via rotation during the time of the acquisition[56], then the cardiac deformation is assumed to be treated locally as a rigid body. The attenuation given by Eq. 15 is:
 ,
,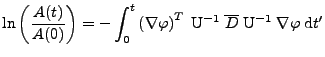 .
.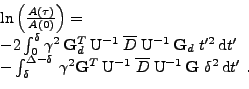


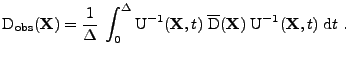
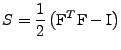 ,
,
![]() are used. The tensor
are used. The tensor
![]() is expressed in the new coordinate system by the relation given in Eq. 24.
The density flux
is expressed in the new coordinate system by the relation given in Eq. 24.
The density flux
![]() can be expressed as in the case of the Cartesian coordinates (see beginning of appendix F).
can be expressed as in the case of the Cartesian coordinates (see beginning of appendix F).
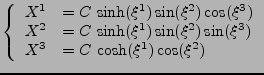
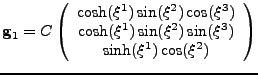

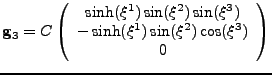 .
.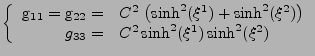
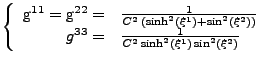
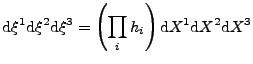
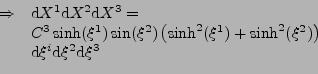

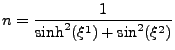
![\begin{displaymath}\begin{array}{*{2}{l}}
{\bf M}_{,t}=
&
\displaystyle
{\bf...
...{,k}
\right)
\Bigr)
\biggr]
\Biggr)
\mbox{ .}
\end{array}\end{displaymath}](img249.png)
![]() is introduced [57,58]:
is introduced [57,58]:
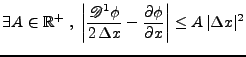 .
.![$\displaystyle [\mathscr{D}^1]_{i,j}=
\left\{
\begin{array}{rl}
1 & \mbox{if ...
... \\
-1 & \mbox{if }\;\; i=j+1 \\
0 & \mbox{otherwise}
\end{array}
\right.$](img263.png)
![$\displaystyle [\mathscr{D}^{11}]_{i,j}=
\left\{
\begin{array}{rl}
1 & \mbox{...
...j \\
1 & \mbox{if }\;\; i=j+1 \\
0 & \mbox{otherwise}
\end{array}
\right.$](img264.png)
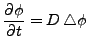 ,
,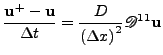 ,
,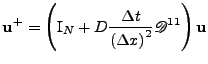 ,
,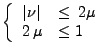 ,
,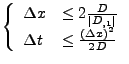 .
.![\includegraphics[width=6.0cm]{picture/fig_diffusion_implicit_1D_init.eps}](img293.png)
![\includegraphics[width=6.0cm]{picture/fig_diffusion_implicit_1D.eps}](img294.png)
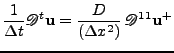 ,
,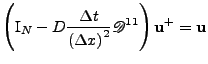 ,
, ,
,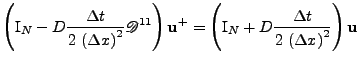 ,
, .
.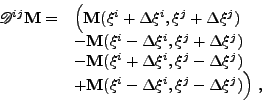
![\begin{displaymath}\begin{array}{l}
M^i(k_1\Delta\xi^1,k_2\Delta\xi^2,k_3\Delta...
...1+N_1\left(k_2+N_2\,k_3\right)\right)]
\mbox{ .}
\end{array}\end{displaymath}](img315.png)
![\begin{displaymath}\begin{array}{l}
[\mathscr{D}^{12}]_{I,J}=
\\
\left\{
\b...
...\\
0
&
\mbox{ otherwise}
\end{array}
\right.
\end{array}\end{displaymath}](img322.png)
![\begin{displaymath}\begin{array}{l}
[\mathrm{G}]_{I,J}=
\\
\left\{
\begin{a...
...\\
0 & & \mbox{ otherwise}
\end{array}
\right.
\end{array}\end{displaymath}](img326.png)
![\begin{displaymath}\begin{array}{l}
[\mathrm{P}^m]_{I,J}=
\\
\left\{
\begin...
...\\
0 & & \mbox{ otherwise}
\end{array}
\right.
\end{array}\end{displaymath}](img333.png)
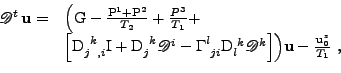
![\begin{displaymath}\begin{array}{*{2}{l}}
\mathcal{S}=&
\mathrm{G}-\frac{\math...
...athrm{D}}{_l^k}\mathscr{D}^{k}
\right]
\mbox{ ,}
\end{array}\end{displaymath}](img338.png)
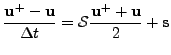 .
.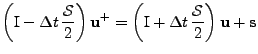 ,
,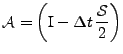 ,
,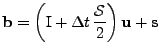 .
.![]() as a parameter of the coordinate system through time.
The equation expanded in the new coordinate system is linear and the diffusion part makes this equation parabolic.
as a parameter of the coordinate system through time.
The equation expanded in the new coordinate system is linear and the diffusion part makes this equation parabolic.
![]() calculations [61] where
calculations [61] where ![]() is the size of the matrix, which is given by
is the size of the matrix, which is given by
![]() and where each
and where each ![]() gives the size in each dimension
gives the size in each dimension ![]() ,
, ![]() , and
, and ![]() . Least squares and conjugate gradient methods enable the process to be sped up; however, for large systems where
. Least squares and conjugate gradient methods enable the process to be sped up; however, for large systems where
![]() , the iteration process becomes very slow.
More research on implementing an Alternative Direction Implicit (ADI) scheme should be performed. Then each iteration should follow three passes but the matrix on the left hand side of the equation becomes tridiagonal and could be rapidly inverted using the Thomas algorithm [58,60].
, the iteration process becomes very slow.
More research on implementing an Alternative Direction Implicit (ADI) scheme should be performed. Then each iteration should follow three passes but the matrix on the left hand side of the equation becomes tridiagonal and could be rapidly inverted using the Thomas algorithm [58,60].
![]() at the time of the acquisition, is given by Eq 19 where the tensor
at the time of the acquisition, is given by Eq 19 where the tensor
![]() is given by:
is given by:
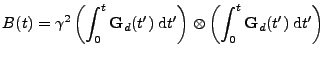 .
.
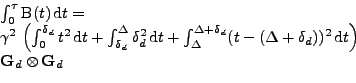
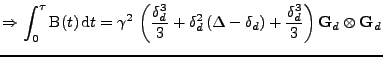 .
.![$\displaystyle \tensor{[\mathrm{B}\mathrm{D}]}{_i^j}=\sum_{k=1}^{3}v_i\,v^k\,\tensor{\mathrm{D}}{_k^j}$](img367.png)
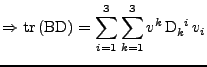 .
.![$\displaystyle {\bf v}^T\mathrm{D}{\bf v}
=
\sum_{j=1}^{3}
\left[
\left(
\sum_{k=1}^{3}
v^k\,\tensor{\mathrm{D}}{_k^j}\right)v_j
\right]$](img369.png)
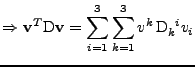 .
. .
.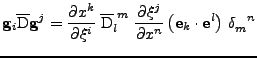
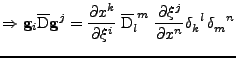

 ,
,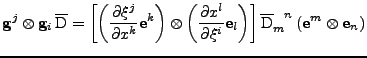
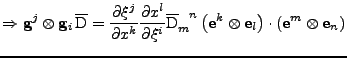 .
.
 .
.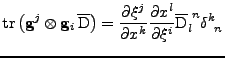
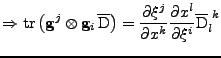
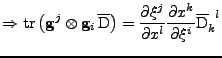 ,
,![]() .
Using the relation
.
Using the relation
![]() given by derivation
given by derivation
![]() is orthonormal, the contravariant and covariant vectors are equal meaning
is orthonormal, the contravariant and covariant vectors are equal meaning
![]() .
Moreover, this basis doesn't depend on the position
.
Moreover, this basis doesn't depend on the position ![]() , therefore:
, therefore:
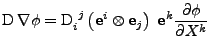 .
.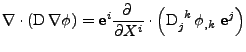 .
.![]() with covariant basis vectors
with covariant basis vectors
![]() , contravariant basis vectors
, contravariant basis vectors
![]() , and contravariant metric tensor
, and contravariant metric tensor
![]() , the expression of the diffusion is given by:
, the expression of the diffusion is given by:
![$\displaystyle \nabla\cdot\left(\mathrm{D}\,\nabla\phi\right)
=
\left[
\left(...
...{\Gamma}{^l_{ji}}\tensor{\mathrm{D}}{_l^k}\,\phi_{,k}
\right]
\mathrm{g}^{ij}$](img418.png) ,
,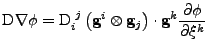
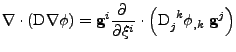 .
.![$\displaystyle \nabla\cdot\left(\mathrm{D}\nabla\phi\right)
=
{\bf g}^i
\left...
...{,i}\;{\bf g}^j
+
\tensor{\mathrm{D}}{_j^k}\phi_{,k}\;{\bf g}^j_{,i}
\right]$](img426.png) .
.![$\displaystyle \nabla\cdot\left(\mathrm{D}\nabla\phi\right)
=
{\bf g}^i
\left...
...tensor{\mathrm{D}}{_j^k}\,\phi_{,k}\;\tensor{\Gamma}{^j_{li}}{\bf g}^l
\right]$](img427.png)
![$\displaystyle \Rightarrow
\nabla\cdot\left(\mathrm{D}\nabla\phi\right)
=
\le...
...{\Gamma}{^l_{ji}}\tensor{\mathrm{D}}{_l^k}\,\phi_{,k}
\right]
\mathrm{g}^{ij}$](img430.png) ,
,