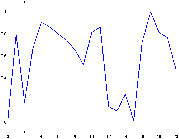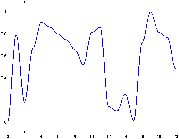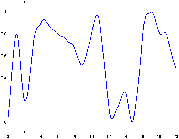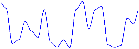Rohmer damien
Cedric Rousset
Modelisation de la forme des vagues
Table des matières
La visualisation de surface fluide est aujourd'hui encore un sujet de recherche complexe et pour lesquel les applications sont toujours plus nombreuses. Afin de réaliser la visualisation d'une surface donnant l'impression de vagues en un temps raisonnable des méthodes basées sur des approches physique ou non peuvent être développées.
Les deux méthodes possèdent chacune des avantages et, avoir la possibilité d'utiliser la meilleur des deux permet des visualisations à la fois réaliste et robustes d'un point de vue physique.
Les équations générales de la mécaniques des fluides ont alors étés reprises et des hypothèses simplificatrices ont été posées afin d'obtenir une solution exprimable algébriquement de façon paramétrique. Une implémentation en temps réel a alors permis de tester le modèle dans des cas simples.
Ensuite, une approche basée sur le bruit de Perlin et une variante de celui-ci a été mise en place. Celle-ci s'est également réalisée dans une approche temps réel et permet de modéliser correctement l'aspet complexe de l'eau. Enfin, une visualisation de cette méthode plus lente réalisée par ray-tracing a également été réalisée et permet la visualisation de vagues d'une grande complexité ayant un aspect naturel.
Abstract
Fluid visualization is still a complex research area in which the number of applications are increasing. In order to set up a visualization giving the apearance of the water waves in a resonnable amount of time, differents methods based or not on the physic can be developped.
Both methods have advantages and the possiblity to use the best from them enable realistic and robust visualizations from a physical point of view.
General equations from fluid mecanics were used and hypothesis followed by simplifications enabled to get an parametric algebraic expression of the solution. Then, a real time implementation enable to test the given model in some simple cases.
Next, an approach based on the Perlin noise and a non linear combination of it was set up. This was performed in real time and enables to get the complex apperance of the water.
Finally, a slower ray traced visualization was applied to the previous method and gives the possiblity to visualize realistic and highly complex liquid waves.
1 Introduction
La modélisation des milieux fluides dans le but de leur visualisation est d'un grand attrait pour de nombreux domaines allant de l'aspect ludique des images de synthèses dans les films jusqu'au modèles de fluides utilisés en imagerie médicale.
Cependant, bien que les équations physiques consitutives soient bien connues, elles sont très complexes à résoudre car elles sont fortements non linéaires. De plus la résolution numérique est difficile car elles sont instables. Les méthodes de rendues sont donc généralement obtenues par simplifications. Et les visualisations en temps réelles sont largements basées sur des modèles extrèmements simples.
Ce projet se place dans le cadre de la visualisation de surface liquide. En prennant l'exemple de la modélisation de la forme de vagues telles qu'on peut les voir sur un lac ou en mer. Le rapport présent ne consitue qu'une approche et un survol non exaustif de quelques méthodes déja utilisées dans ces domaines. Le fil conducteur que nous tenterons de suivre sera de se donner les moyens de la mise en place d'une visualisation d'un fluide d'aspect réaliste mais ayant la possibilité de se baser sur un fondement physique robuste.
Pour satisfaire ce but, nous partirons des équations générales de la physique des fluides dans la première partie (chap. 1) et réaliserons alors des simplifications contrôlées de ces équations pour obtenir une solution certe simple et applicable dans des cas particuliers mais dont le fondement physique est établie (chap. 2).
Dans une seconde partie du rapport, nous nous interesserons à l'établissement d'un aspect réaliste complexe de la surface par des moyens rapides et non physiques. Pour cela, nous étudierons un type de bruit particulier (chap. 3) et en réaliserons une implémentation sous OpenGL. Finalement, nous implémenterons une méthode de visualisation de bonne qualité par ray-tracing (chap. 4) permettant d'avoir une impression de liquide réaliste.
2 Théorie
3LA
théorie traitant des fluides est un vaste domaine qui peux être couvert sur de nombreux aspects. La littérature traitant de mécanique des fluides est très abondante et les sujets abordés sont très larges en partant de la modélisation physique, par la recherche de l'existence de solutions mathématiques aux équations complexes régissant la dynamique du fluide, en passant par les méthodes de représentation. Dans ce projet, nous nous efforcerons de nous rammener à l'aspect visualisation de ce fluide.
En effet, au niveau de l'aspect visualisation et modélisation informatique, les fluides peuvent rentrer dans la classe appelée de “modèle déformable”. On a ainsi un volume/surface qui peut se déformer sous l'action de forces (internes ou externes).
On peux noter deux grands types de modèles déformables au niveau de la simulation de phénomènes physiques: les modèles de matériaux solides et les modèles de fluides (gaz y compris).
Dans la première classe, on peut y noter la déformation des objets courants tels que les animaux, personnages, .... Cette classe ayant un interêt dans le cadre de la visualisation pour des scènes animées (jeux vidéo, films, ...). L'animation de tissus également est un domaine à part entière. On notera par exemple l'utilisation de techniques évolués dans certains films comme star-wars, où les costumes de certains personnages sont totalement fictifs et réagissent cependant avec un réalisme surprenant. Du coté de la recherche médicale, on peut également noter la forte demande de modélisation de modèles déformables pour les organes afin de modéliser leur déformations dans le corps, et, par exemple, l'effet de la coupure due à l'insision par le bistourie du chirurgien.
D'un autre coté, les modèles fluides sont différents par leur approches de la déformation qui n'est pas visible en tant que telle. Cependant il s'agit toujours d'un système de référence subissant une déformation due à l'action de forces diverses. L'application de la visualisation de fluides peut également être ludique. En effet, films et jeux vidéos demandant une approche toujours plus réaliste sur le plan visuel. Cependant la demande de la recherche pour des méthodes de résolution de problèmes de mécanique des fluides est également très importantes. Des modèles de refroidissements de centrales nucléaires au modèle du mouvement du coeur prenant en compte la circulation du sang, en passant par l'optimisation des formes aérodynamique des ailes d'avions, la mécanique des fluides entre en jeu dans un nombre incalculable de domaines. L'apect visualisation est donc évidemment à prendre en compte dans la comprehension des phénomènes très souvent complexe de ces domaines. Si le réalisme naturel de la visualisation n'est pas forcément l'aspect demandé, une partie de la visualisation est toujours mise en avant.
2.1 Notations
Dans l'ensemble de ce rapport nous utiliserons quelques conventions de notation.
Premièrement les vecteurs seront différenciés des scalaires par des lettres en gras v=v.
Dans l'espace 3D repérés par les coordonnées x,y,z, nous utiliserons indifférement suivant les situations la notation (x1,x2,x3)=(x,y,z) lorsque la notation peux se simplifier (cas de la somme notamment).
En considérant la base Euclidienne de l'espace, nous notterons donc
On utilisera, afin de simplifier les notations, également le vecteur r pour ne désigner que les deux composantes (x,y) qui seront quelquefois utilisés de façon séparés de z pour définir la surface.
2.2 Mécanique
Dans un premier temps, les fluides sont introduits par leur modèle physique et théorique afin de comprendre ce que l'on cherche à modéliser.
On note premièrement que les fluides, comme les objets, sont soumis aux lois de la mécanique. On rapelle qu'il existe plusieurs types/niveaux de mécanique:
-
Mécanique du point matériel. Cette mécanique s'adresse à des points (en interactions ou non) de dimensions nulles. Dans cette hypothèse, seul trois degrés de libertés sont présents pour chaque point. Ces degrés correspondent aux translation suivant x,y et z (la rotation n'ayant pas de sens pour un point de dimension 0).
Dans cette hypothèse, la loi fondamentale s'appliquant dans le cas classique est celle de Newton stipulant que:
où m est la masse de la particule, a son accélération dans un référentielle Galiléen, Fk les forces extérieures exercées sur la particule, et x la position de celle çi.
On notera également que, connaissant à chaque instant t la position x(t) de la particle, on peut relier son accélération à sa position par une simple dérivé seconde:
En remplaçant cette équation dans la précédente, on obtient une équation différentielle du second ordre. On remarquera qu'en toute généralité, F peut également dépendre comme paramètre des dérivés de x par rapport au temps. Cette partie simple de la mécanique peut donc déja faire intervenir des équations différentielles ordinaires non linéaires et complexes. Un exemple simple étant le problème à trois corps dont la solution analytique n'existe pas, et dont la solution numérique possède un comportement chaotique (la moindre perturbation initiale va entrainer un changement très important de la solution lorsque t croît).
- Mécanique des systèmes rigides. Dans ce cas, on ne considère plus un unique point, mais un solide rigide pouvant être en mouvement. On a alors 6 degrés de libertés en notant les trois translation et les trois rotations. Ce système s'adresse en particulier aux mouvements de robots automatiques. Chaque partie peut être modélisée par des jointures d'un type donné (glissière, pivôt, encastrement, ...). Chaque jointure limitant le nombre de degré de liberté. On peut donc connaître le comportement du système lorsque l'ensemble des translations et angles sont définis.
L'aspect dynamique fait, de plus, intervenir un ensemble de moments dépendant de la distribution de masse dans ce solide. On notera l'exemple des moments d'inertie s'opposant aux variations de la rotation du solide. Les équations régissant la dynamique font donc appels à la loi de Newton plus l'équation des moments d'inertie.
- Mécanique des milieux continus. Dans cette dernière mécanique, on considère que l'on a non seulement les déformations solides: translation, rotation et même aggrandissement, mais également toutes déformations internes. Ainsi les positions relatives des points à l'intérieur des matériaux ne sont plus fixes mais dépendent de leurs emplacements initiaux et du temps.
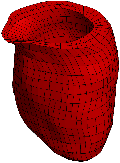
Dans ce cas, les variations dynamiques dépendent non seulement du temps, mais également de la position. Les équations régissant ces systèmes sont donc des équations aux dérivés partielles (PDE). Celle çi sont évidement très complexes à résoudre, et, à l'exception de quelques cas très simples, les solutions analytiques n'existent pas. Un exemple de milieu déformable d'un coeur est montré en fig. 1
Fig. 1: [
Exemple d'un modèle déformable]Exemple d'un modèle déformable correspondant ici à un modèle informatique d'un ventricule d'un coeur.
2.3 Approche Lagrangienne et Eulerienne
La mécanique des milieux continus englobe les solides et liquides. Cependant une distinction importante les séparent dans le traitement de leurs équations.
L'approche Lagrangienne est probabalement la plus simple à comprendre. Elle correspond au cas des solides déformables.
Dans ce cas, le solide est défini initialement dans un référentiel R0 correspondant à son état de départ (en général état sans tensions internes appelé “stress free”).
L'ensemble des positions x0 de l'objet peut donc être défini dans ce référentiel.
Lorsque le temps évolue, les positions sont déformées les une par rapport aux autres par une fonction ϕ telle que x=ϕ(x0), avec x correspondant aux nouvelles positions d'un point donné.
Dans cette approche, chaque point du solide est suivi lors de son déplacement. À chaque instant t on peut donc définir pour chaque point du référentiel original, sa nouvelle position suite à la déformation.
La vitesse d'un point P est donc défini simplement par
et de même, son accelération par
Les forces s'appliquant sur l'objet sont par contre plus complexes à modéliser. Celle-ci dépendent notamment, dans le cas général, de l'orientation. Ces forces sont alors caractérisées par des tenseurs (“stress”) et la déformation du solide (déplacement des positions les une par rapport aux autres) sera caractérisé par un autre tenseur (“strain”);
Dans le cas des fluides, l'approche est différente. On rappelle premièrement qu'en mécanique des fluides, une particule de fluide correspond à un ensemble mésoscopique1 constitué de molécules d'eaux.
En effet, à l'echelle macroscopique, une particule fluide comme illustré en fig. 2 doit avoir une dimension très petite comparée à la taille du volume étudié.
Fig. 2: [
Exemple de particules fluides]Exemple de particule fluide.
Par contre, cette particule, à l'echelle microscopique doit contenir un nombre très important de molécules d'eau afin de bien correspondre à l'approximation d'un milieu continu.
Chaque particule de fluide possède une position donnée à un temps t fixe. Cependant, lorsque le temps évolue, il n'est pas possible de connaître la position suivante de cette particule. Ainsi au contraire de la mécanique du solide (où l'on pouvait positionner des marqueurs sur l'objet), les fluides se prettent mal au suivi de particules.
Dans ce cas, on adopte une autre méthode de caractérisation appelée méthode Eulerienne: Pour chaque positions fixés d'un repère R (quelque soit le temps), on fournit la vitesse du fluide en ces points.
On peut remarquer que les deux approches se rejoignent par les lignes de flux. En effet, en définissant une particule située à une position x0 au temps t=0, on peut, connaissant la vitesse en tout point et à tout instant, obtenir la trajectoire de cette particule par intégration de la vitesse:
|
x |
(t)= |
∫ |
|
v(x(t')) dt'
,
(5) |
-
le terme lié à la dérivation temporelle qui est appelé dérivé locale
- le terme lié à la dérivation spatialle appelé terme de dérivé convective.
On remarquera que le terme d xi/d t repésente les composantes de la vitesse.
On peux donc écrire l'équation sous la forme d'un produit scalaire
|
a(x,t)= |
|
(x |
,t)+ |
|
vk(x,t)⋅ |
|
(x,t)
.
|
2.4 Equation de la dynamique
Les équations de la dynamique peuvent maintenant être écrites par simple application du principe de Newton. Pour cela, il suffit d'appliquer l'equation sur l'ensemble des particules du fluide:
|
|
∫ |
|
⎡
⎢
⎢
⎣ |
ρ(x,t) |
|
(x,t)+ |
⎛
⎝ |
v(x,t)⋅∇ |
⎞
⎠ |
v(x,t) |
⎤
⎥
⎥
⎦ |
dx |
= |
∫ |
|
|
Fk(x,t) dx
,
(8) |
|
F |
p(t)= |
∫ |
|
p(x,t) (−n(x,t)) dx
,
|
|
|
⎧
⎪
⎪
⎨
⎪
⎪
⎩ |
|
|
|
+ |
⎛
⎝ |
v⋅ ∇ |
⎞
⎠ |
v=− |
|
+μ∇2v+f |
|
| |
|
∇⋅v=0
|
|
|
(9) |
2.5 En résumé
-
La dynamique des fluide correspond au cas de la mécanique des milieux continus avec un point de vue Eulerien.
- L'équation de Navier-Stockes provient de l'application du principe fondamentale de la dynamique sur une particule de fluide.
- Chaque terme de l'équation peut être simplifié suivant les hypothèses prises en compte.
3 Approche pseudo-physique de la forme des vagues
The wrong solution of the right equation;
The right solution of the wrong equation.
Feng Kang, Beijing Sept. 1, 1992
3APRÈS
avoir mis en place la partie des équations physiques, nous allons dans cette partie utiliser un modèle provenant d'approximations assez grossières mais permettant d'obtenir une première approche du mouvement d'un fluide qui, comme nous allons pouvoir le constater, permet de modéliser de façon très simple une vague, mais n'est malheureusement pas le modèle généralement utilisé.
3.1 Forme de vagues
Nous allons tout d'abord essayer de prendre en compte le modèle extrèmement simpliste utilisé dans des visualisations de type temps réels et nous allons essayer de comprendre pourquoi ce choix ne possède pas de fondement physique.
3.1.1 Forme sinusoidale
Nous allons donc nous intéresser à une étendue liquide de type surface d'océan. On recherche alors à représenter les vagues se propageants sur la surface libre de cette étendue d'eau.
Le point de vue le plus simple consiste à considérer une surface de type “height field” (ou champ de hauteur) η:(x,y)↦(x,y), avec (x,y) parcourant la surface de l'océan (soit (x,y)∈R2) et η représentant la hauteur de la surface. Cette représentation permet de représenter n'importe quel type de vagues dans la limite où la fonction n'est pas multivaluée (le cas des vagues se brisants représente une fonction multivaluée).
On peut alors penser aux premières représentations informatique de surfaces d'eau où le liquide était simplement représenté par des oscillations se répétant indéfiniements (notamment en 1D).
On peut ainsi donner une impression grossière de vagues en faisant osciller une surface grâce à une fonction sinusoïdale. Ce modèle est très répendu et permet une approche temps réel de façon évidente.
Dans le cas monodimentionel, on peut donc considérer η:x↦ A sin(x+φ), où A est la hauteur de la vague. Ensuite, l'animation de l'eau se réalise simplement en translatant cette fonction le long de l'axe x à la vitesse constante u avec la fonction η:(x,t)↦ A sin(x+φ−u t).
De même, on peut réaliser très simplement cette méthode pour le cas de 2 dimensions. Pour cela on note r le vecteur position r=(x,y). On considère un sinus dans la direction k=(kx,ky). On obtient donc la relation η(r)=A sin(k⋅ r+φ). Et finalement, l'évolution temporelle de la vague dans la direction k est donnée également par sa translation le long de k à la pulsation ω par
η(r,t)=A sin(k⋅ r−ω t+φ)
(10)
On pourra remarquer que l'utilisation d'un sinus unique fournit une impression de répétitivité ne pouvant pas prétendre à un aspect réaliste de la surface. Pour cela, on peut considerer un nombre de vagues plus important, chacune ayant une direction ki, une vitesse de propagation vi et une phase φi.
La fonction hauteur de vague peut donc être représentée par
|
η(r |
,t)= |
|
Ai sin(ki⋅ r−ωi t+φi)
(11) |
3.1.2 Quelle équation résolvons nous?
On peut initialement supposer que l'on a une relation linéaire entre ∥ki∥ et ωi.
On note alors
∀ i, ∥ki∥=μ ωi
On peut alors remarquer qu'en calculant le laplacien de η:
|
△ η(r |
,t)=− |
|
∥ki∥2 Aisin(ki⋅ r−ωi t+φi)
|
|
⇒ △ η(r |
,t)=− μ2 |
|
ωi2 Aisin(ki⋅ r−ωi t+φi)
|
η(r,t)=F(k⋅r−ω t)
.
L'équation est linéaire et ne correspond pas à celle des fluides. Par contre, elle a l'avantage de modéliser la propagation de façon simple. Cette équation est donc encore souvent la base des méthodes de visualisation dans les rendus temps réel car la solution nécessite peu de calculs pour la machine.
Par la suite, l'équation peut être modifiée. En effet, si l'on fait maintenant dépendre ω de k de façon non linéaire, on obtient alors une équation de dispersion, avec des longueurs d'ondes dépendant de la fréquence.
3.2 Mise en place de la dispersion
Nous avons donc pu constater que l'équation simple de propagation utilisé lors du déplacement de la hauteur de la vague, bien que souvent utilisé, n'est pas correct d'un point de vue physique. Nous allons donc, bien qu'en restant proche de cette forme, tenter d'obtenir une relation possédant quant à elle un fondement réel.
Premièrement, on rapel les notations utilisées.
Soit l'expression:
f(r,t)=Asin(k⋅r−ω t)
Le vecteur k est appelé le vecteur d'onde et ∥k∥ le nombre d'onde. Ce nombre d'onde est relié à la longueur d'onde spatiale λ de la vague par ∥k∥=2π/λ. La direction de k indique alors le sens de propagation de cette vague.
ω quant à lui représente la pulsation de la vague. Elle est reliée à la fréquence temporelle de celle-ci par ω=2π f et à la période τ=1/f.
Pour une fréquence donnée, on note la vitesse de l'onde (vitesse de phase) par
où uk représente la direction de propagation k/∥k∥.
Pour le cas d'une multitude de fréquences, la vitesse de chaque pulsation n'est plus visible. On a alors accès à la vitesse de groupe correspondant à la vitesse de déplacement de l'enveloppe définie par
avec la notation un peu abusive d'une dérivation par un vecteur correspondant à la dérivation par rapport à chacune de ces composantes.
Évidemment, lorsque ∥c∥≠ ∥cg∥, la propagation est dispersive et la relation entre ∥k∥ et ω n'est pas linéaire.
3.2.1 Condition de pression à la surface
Revenons maintenant à l'équation de Navier-Stockes pour les fluides parfaits Newtonniens incompressibles:
|
|
⎧
⎪
⎪
⎨
⎪
⎪
⎩ |
|
|
|
+ |
⎛
⎝ |
v⋅ ∇ |
⎞
⎠ |
v=− |
|
+μ∇2v+f |
|
| |
|
∇⋅v=0
|
|
|
|
|
⎛
⎝ |
v⋅ ∇ |
⎞
⎠ |
v
=
|
|
∇ |
⎛
⎝ |
v⋅v |
⎞
⎠ |
−v× |
⎛
⎝ |
∇×v |
⎞
⎠ |
|
|
|
+ |
|
∇ |
⎛
⎝ |
v⋅v |
⎞
⎠ |
+ |
|
−g=0
.
(12) |
∇ ϕ=v
.
On peut alors traduire la relation d'incompressibilité sur ce potentiel en écrivant:
On reconnaît alors l'expression du Laplacien. Ainsi ce potentiel vérifie l'équation de Laplace:
△ ϕ(r,t)=0
Considérons à nouveau l'equation 12, en introduisant ce potentiel, on obtient alors
|
∇
|
⎛
⎜
⎜
⎝ |
|
|
+ |
|
⎛
⎝ |
v⋅v |
⎞
⎠ |
+ |
|
+g z
|
⎞
⎟
⎟
⎠ |
=0
,
(13) |
3.2.2 Equation de la surface libre
Dans la suite, nous allons nous interesser spécifiquement à l'interface air-eau. Cette interface est donc représentée par une surface évoluant au cours du temps
η:(t,x,y)↦ η(t,x,y)
.
Nous avons donc en tout point de la surface à un instant donné z=η(t,x,y)=η(t,r), où l'on rapelle que l'on note maintenant r=(x,y).
On va maintenant réaliser l'hypothèse que le volume de l'eau n'entre pas en compte. Seule la surface va jouer un rôle.
On note alors la quantitée G(t,r)=z−η(t,r). Pour un élément de fluide sur la surface, la fonction G doit évidement rester nulle. C'est à dire que sa variation par unité de temps est nulle également.
Ici, la différentielle exacte doit être pris en compte comme une dérivé convective (voir eq. 7 du chap. 2.3), cela conduit donc à la relation suivante
On peut alors développer cette expression
Puis on note les relations provenant de la définition de G
Ce qui fournit donc l'equation différentielle suivante sur la surface libre
3.2.3 Dispersion
On résume donc les equations obtenues en eq. 14 et 15.
Ces 2 relations correspondent donc à la version simplifiée de Navier-Stockes pour le cas d'une surface libre. Les équations aux derivés partielles sont cependant toujours non linéaires et restent complexes.
On va alors les simplifier très fortement en les linéarisants par rapport à leurs positions de repos. On va donc considérer uniquement de très faibles variations sur η, et v. Les positions de repos sont considérées comme étant données pour z=0 et v=0.
On obtient alors les équations linéarisées très simples suivantes:
|
|
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩ |
|
| |
|
|
|
(t,x,y,є)
+
g η(t,x,y,є)
=
0
|
|
|
|
η= Acos(k⋅r−ω t)
,
On recherche alors ϕ sous la forme
ϕ=f(z) sin(k⋅ r−ω t)
On utilise alors l'equation de Laplace que doit satisfaire ϕ:
△ ϕ=0
La solution de cette equation est bien connue et se représente sous la forme d'exponentielle
f(z)=C e∥k∥z + D e−∥k∥z
.
On suppose que le plan d'eau possède une profondeur infinie. On suppose donc que ϕ, et par là f, va rester borné pour z tendant vers −∞. On a donc D=0. On obtient donc
ϕ = C e∥k∥ z sin(k⋅ r−ω t)
.
On peut donc écrire également vz=C ∥k∥ e∥k∥ z sin(k⋅ r−ω t) avec la relation v=∇ ϕ.
Afin de trouver la relation de dispersion, on introduit cette expression dans les equations linéarisées du plan d'eau et on prend z=0. On obtient alors les relations suivantes
Soit
qui correspond bien à la relation de dispersion annoncée.
On peut alors écrire également le potentiel scalaire par
Et la vitesse de déplacement d'une onde à une fréquence donnée est ainsi de
Et la vitesse de groupe due à cette dispersion est donc
On pourra remarquer que cg=1/2c.
On obtient donc la relation de dispersion pour les ondes dites d'ondes de gravitées car elles sont créés par l'action de la gravitée uniquement.
On remarque que l'on a cg≤ c. Cette relation signifie donc que les front d'ondes vont voyager plus rapidement que le groupe lui même. Ainsi les sommets des vaguelettes vont venir se former derrière le groupe d'onde, le parcourir, puis disparaîte à l'avant de celui ci.
Une vidéo fournit en annexe (1 movie gravity wave) illustre notament ce principe dans un cas unidimensionel simple où l'on peut voir la propagation d'un front d'onde.
3.2.4 Ondes de capillaritée
Il est généralement considérée une autre action sur la surface. Celle-ci est due à l'action de la tension superficielle de la surface de l'eau. Cette force est notamment celle qui permet aux bulles de savons d'être sphériques. Cette force de tension donne donc l'aspect sphérique aux gouttes d'eau et est donc évidement reliée à la courbure de la surface.
Ces ondes de capillaritées jouent un rôle lorsque la surface possède une courbure importante, c'est à dire pour des longueurs d'ondes faibles (typiquement inférieur à 1.7cm). Cette force tente donc d'empécher une goutte d'être séparé en deux comme l'illustre la figure 3.
Fig. 3: [
Illustration de deux particules fluides acollées]Illustration de deux particules fluides. La tension capillaire tente d'empécher les deux particules de se séparer.
Cette force de tension superficielle agit au niveau de la composante tangentielle de la surface. Cette action T est dirigée de facon à rendre la surface la plus lisse possible et possède les dimensions d'une force par unitée de longueur.
On a donc 2 composantes tangentielles telles que
On suppose encore que les ondes sont d'amplitudes très faibles. C'est à dire que l'on approxime T à sa composante tangentielle. Il faut donc que ∥T∥ ≫ Tz.
On calcule maintenant la variation verticale de cette force de tension superficielle entre deux points infiniement proches:
|
∀ i∈[[0,1]],
t |
|
(r+dr)−t |
|
(r)≃ t |
|
dxi
|
p−p0=t △ η
.
Introduisons alors cette nouvelle pression p dans l'equation de Bernoulli de l'eq. 13 pour obtenir
En recherchant à nouveau une solution de la forme η(t,r)=Acos(k⋅ r−ω t), il suffit alors de remplacer dans les résultats précédents g par g+t/ρ ∥k∥2.
La relation de dispersion est donc trouvée de la même façon, et l'on obtient
La vitesse de phase est cette fois donnée par
et la vitesse de groupe est
Cette fois on a deux types de comportements différents suivant la longeur d'onde. Pour les grandes longeurs d'ondes (typiquement de l'ordre de quelques centimètres), la contribution des ondes de capillarités va être négligeable et l'on va retrouver le comportement des ondes de gravités.
Un rapide calcul montre qu'il faut pour cela
En circonstance normale, on peut considérer g=9.8 kg m/s2, t=0.072 kg/s2 et ρ=103 kg/m3.
Soit dans ce cas λ≫ 1.7 cm.
Dans le cas contraire, les ondes de capillarités dominent. La relation de dispertion est alors approximée par
et les vitesse de phases et de groupes sont telles que
La relation cg=3/2c, montre que cette fois c'est la vitesse de groupe qui se propage le plus rapidement.
Ainsi pour le cas de faible longueurs d'ondes (goutte d'eau, ondes créés par un son fort), les crêtes vont se propager de l'avant vers l'arrière par rapport au sens de propagation du groupe d'onde.
De même, une vidéo fournit en annexe (2 movie capillarity wave) illustre la propagation dans le cas d'ondes de capillarités.
Après avoir mise en place les équations théorique simple, nous allons passer en revue certains modèles utilisés pour représenter la Houle.
3.3 Modélisation de la Houle
Nous avons pu voir que que les solutions obtenues dans le cas des trochoïdes étaient de la forme (en prenant cette fois z≠ 0):
|
|
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩ |
| r=r |
0+ |
|
Ai |
|
e∥ki∥ z0 sin(ωi t−ki⋅r0) |
|
| |
| z=z0+ |
|
Ai e∥ki∥ z0 cos(ωi t−ki⋅ r0) |
|
|
|
3.3.1 Courbes Trochoïdes
On désigne par trochoïde la courbe décrite par un point d lié à un cercle de rayon R roulant sans glisser sur une droite.
|
|
⎧
⎨
⎩ |
| x= R t+d sin(t) |
| |
| y= R +d cos(t) |
|
|
On peut aussi définir la courbe trochoïdes comme une trajectoire composée d'un mouvement rectiligne uniforme et d'un mouvement circulaire de paramétrisation complexe:
On peut faire le lien entre les 2 modèles avec d = r et R=V/ω
-
Pour d = 0 le point est le centre du disque, le trochoïde est alors une droite.
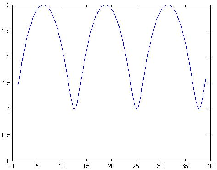
- Pour d < R ou v > rω La courbe s'appelle aussi cycloïde raccourcie et ressemble à une sinusoïde.
Fig. 4: [
trochoïde raccourcie ]trochoïde raccourcie avec R=1 et d=0,5
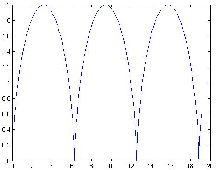
- Pour d = R ou v = rω On obtient la cycloïde.
Fig. 5: [
Cycloïde]cycloïde avec R=1 et d=1
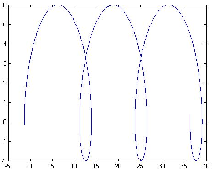
- Pour d > R ou v < rω La courbe s'appelle aussi cycloïde allongée et peut prendre diverses formes, avec de plus en plus de points doubles à mesure que d augmente
Fig. 6: [
trochoïde allongée]trochoïde allongée avec R=2 et d=4
Nous avons faits l'approximation de faibles amplitudes pour la résolution de l'équation de Navier-Stokes. Nous allons donc étudier le phénomène de houle correspondant parfaitement à ces conditions [12, 13].
3.4 Le phénomène de houle
Définition:
-
La houle est un mouvement ondulatoire de la mer formé par une succession de vagues qui ne se brisent pas.
- Une houle se caractérise par son amplitude (en mètres) et sa longueur d'onde λ ou sa période (en secondes).
- Souvent, à peine sensible en pleine mer, la houle s'amplifie au voisinage de la côte et lorsque la profondeur diminue, elle peut alors atteindre plusieurs mètres et déferler.
(Source Wikipédia)
Nous allons nous intéresser particulièrement au modèle de houle de Gerstner qui se base sur l'utilisation des courbes trochoïdes vues auparavant.
3.4.1 Le modèle de houle de Gerstner (1802)
Comme nous avons fait certaines hypothèses pour la résolution de l'équation de Navier Stokes, le modèle de Gerstner se place aussi dans certaines conditions.
-
Hypothèses sur la nature du fluide:
-
Parfait: viscosité nulle.
- Fluide irrotationnel.
- Tension superficielle négligée.
- homogène: structure uniforme dont les éléments constitutifs sont de même nature ou répartis de façon uniforme (une seule phase).
- Hypothèses sur les conditions aux limites: La pression atmosphérique est constante, le vent ne souffle pas, le fond est horizontal et à profondeur infinie.
- Cambrure: (amplitude/longueur d'onde) doit être inférieure à 1/π.
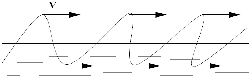
Fig. 7: [
Mouvement de trochoïdes]Illustration d'un mouvement de trochoïdes
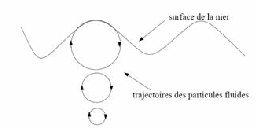
La surface suivra un déplacement dans le sens de rotation des cercles de trochoïdes. Seule l'onde se déplace sur la surface, les particules ayant une trajectoire circulaire fermée autour de leur position de repos.
Le modèle de Gerstner est le premier modèle simple et exact pour la représentation de houle d'amplitude finie. De nombreux autres modèles s'appuient dessus. Nous allons les étudier afin de les comparer et de prendre en compte d'autres paramètres physiques pour la représentation de notre modèle.
Ces modèles ont déjà été utilisés avec succès dans le cas de visualisation comme par exemple dans [14, 15, 16].
3.4.2 Le modèle de houle d'Airy (1845)
Hypothèses:
-
Fluide parfait.
- Fluide irrotationnel.
- Tension superficielle négligée.
- Amplitude doit être très inférieure à la longueur d'onde.
- Amplitude doit être très inférieure la profondeur.
La solution d'Airy est valable pour les ondes de petites amplitudes et les milieux peu profonds. Le mouvement est déduit à partir du développement limité de l'équation de Bernoulli. Cette équation est la loi de la conservation de l'énergie appliquée ici dans le cas d'un fluide irrotationnel.
La fonction F(t) est une constante si on considère une position de repos à l'infini c'est-à-dire que l'on considère que la surface sera sans ondulation. Pour le modèle Airy, on développe au premier ordre d'approximation.
|
|
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩ |
|
| |
| ϕ1= |
|
|
| cosh(∥k∥(z+h)) |
|
| sinh(∥k∥h) |
|
sin(μ) |
|
| |
|
| |
|
|
-
ξ la hauteur de la surface libre par rapport à la position de repos
- ϕ le champ des vitesses
- L la longueur d'onde
Des études en bassin ont démontrés ques la dimension des mouvements des particules est faible par rapport à la longueur d'onde. Ainsi on peut confondre les positions des centres de chaques orbites avec les composantes du vecteur vitesse de la particule.
On obtient finalement les équations suivantes.Cette fois, les trajectoires des particules à la surface libre sont des ellipses.
|
|
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩ |
| r=r0− |
|
|
| cosh(∥k∥ (z0+h)) |
|
| sinh(∥k∥ h) |
|
sin(ω t−ki⋅r0) |
|
| |
| z=z0+ |
|
|
| sinh(∥k∥ (z0+h)) |
|
| sinh(∥k∥ h) |
|
cos(ω t−ki⋅r0) |
|
|
|
Remarques:
-
Les trajectoires sont des ellipses dont le demi-axe horizontal α est constant et le demi-axe vertical β diminue linéairement avec z.
|
|
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩ |
| α= |
|
|
| cosh(∥k∥ (z0+h)) |
|
| sinh(∥k∥ h) |
|
|
| |
| β= |
|
|
| sinh(∥k∥ (z0+h)) |
|
| sinh(∥k∥ h) |
|
|
|
|
- Les trajectoires sont fermées, à la fin de chaque cycle de houle chaque particule revient à sa position initiale. Il n'y a pas de transport de masse. Les particules ne font qu'osciller (ceci n'est valide que pour des ondes de faibles amplitudes).L'eau n'est pas entrainés par l'onde.
- Sur le fond (z = - d = profondeur du fond marin) B s'annule, la trajectoire devient donc un segment de droite.
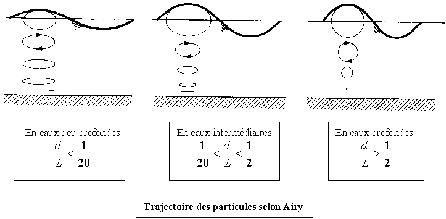
Fig. 8: [
Illustration de la houle d'Airy]Illustration de la houle d'Airy. Les orbites des mouvements circulaires diminuent si la profondeur d'eau diminue ou que les particules sont proche du fond
3.4.3 Le modèle de houle de Stokes (1847)
Dans le modèle de Stokes, les termes non linéaires sont pris en compte. La méthode utilisée, appelée méthode des perturbations, consiste à développer les différentes variables en série de puissance.
En poussant les développements limités à des ordres supérieurs, on obtient les modèles de houle non-linéaire de Stokes. Ces modèles se traduisent par l'ajout d'harmoniques d'orde supérieur.
Stokes d'ordre 2
|
|
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩ |
| ξ2=ξ1+ |
|
|
| 3−tanh(∥k∥h)2 |
|
| tanh(∥k∥h)3 |
|
cos(2μ) |
|
| |
| ϕ2=ϕ1+ |
|
|
| 3−cosh(2∥k∥(z+h)) |
|
| sinh(∥k∥h)4 |
|
sin(2μ) |
|
| |
|
| |
|
|
Stokes d'ordre 3
|
|
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩ |
| ξ3=ξ2+ |
|
|
| 1+8cosh(∥k∥h)6 |
|
| sinh(∥k∥h)6 |
|
cos(3μ) |
|
| |
| ϕ3=ϕ2+ |
|
|
| 11−2cosh(2∥k∥h) |
|
| sinh(∥k∥h)7 |
|
cosh(3∥k∥(z+h)) sin(3μ) |
|
| |
| L= |
|
tanh( |
|
) |
⎛
⎜
⎜
⎝ |
1+∥ki∥2 |
| 14+4cosh(2∥k∥h)2 |
|
| 16sinh(∥k∥h)4 |
|
⎞
⎟
⎟
⎠ |
|
| |
|
|
3.4.4 Le modèle de houle de Biesel
Malgré la prise en compte des faibles profondeurs, le modèle de Stokes ignore l'aspect énergétique de la réfraction sur le fond. Ceci a pour conséquence de l'invalider lorsque les vagues s'approchent du déferlement. En pratique, Le modèle de Stokes n'est plus valable pour des profondeurs inférieures à la moitié de la longueur d'onde.
L'approche de Biesel consiste à tenir compte des modifications d'amplitudes impliquées par la variation de la longueur d'onde selon la loi suivante:
|
|
⎛
⎜
⎜
⎝ |
|
⎞
⎟
⎟
⎠ |
|
= |
| 1 |
|
| tanh(∥k∥ h) |
⎛
⎜
⎜
⎝ |
1+ |
|
⎞
⎟
⎟
⎠ |
|
|
,
|
|
|
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩ |
| r=r0+Ax sin |
⎛
⎜
⎜
⎜
⎜
⎝ |
∫ |
|
k⋅ dr−ω t |
⎞
⎟
⎟
⎟
⎟
⎠ |
−Bxcos |
⎛
⎜
⎜
⎜
⎜
⎝ |
∫ |
|
k⋅ dr−ω t |
⎞
⎟
⎟
⎟
⎟
⎠ |
|
| |
| z=z0+Az sin |
⎛
⎜
⎜
⎜
⎜
⎝ |
∫ |
|
k⋅ dr−ω t |
⎞
⎟
⎟
⎟
⎟
⎠ |
−Bzcos |
⎛
⎜
⎜
⎜
⎜
⎝ |
∫ |
|
k⋅ dr−ω t |
⎞
⎟
⎟
⎟
⎟
⎠ |
|
|
|
En fait, les orbites des particules deviennent des ellipses dont la direction varie suivant la profondeur du fond.
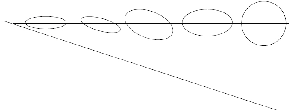
Fig. 9: [
Illustration de la houle de Biesel]Illustration de la houle de Biesel. L'orentation des orbites des mouvements des particules varient en fonction de la profondeur du fond
Cette méthode permet de s'approcher du point de déferlement mais elle reste paramétrique donc on ne pourra en aucun cas représenter la brisure de vague [17].
Maintenant que nous avons vus les différents modèles de houle, nous allons nous intéresser à la représentation numérique de notre modèle
3.5 Le modèle paramétrique
|
|
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩ |
| r=r |
0+ |
|
Ai |
|
e∥ki∥ z0 sin(ωi t−ki⋅r0) |
|
| |
| z=z0+ |
|
Ai e∥ki∥ z0 cos(ωi t−ki⋅ r0) |
|
|
|
Les modèles paramétriques sont des modèles fournissant des équations décrivant paramétriquement la surface à un instant donné. Comme la dynamique générale fournit des équations différentielles, les modèles paramétriques se basent sur des solutions particulières.
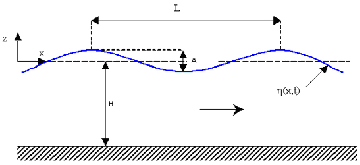
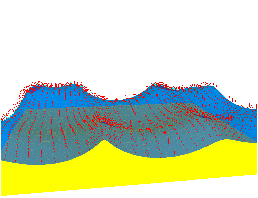
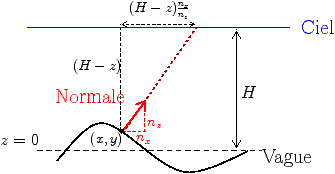
Fig. 10: [
Paramètres pour la modélisation de la houle.]Représentation des paramètres nécessaires à la modélisation de la houle.
3.5.1 Propagation
On note que le rayon décroît exponentiellement avec la profondeur. La courbe résultant des mouvements simultanés des particules dont les centres constituent la courbe continue z = z0 est appelée trochoïde. Par contre, l'utilisation des équations paramétriques données nous limite à une surface de topologie planaire.
3.5.2 Zone de compression
On constate que le mouvement de la particule de fluide ne s'effectue plus seulement selon l'axe verticale z. La particule possède également un mouvement dans le plan horizontal qui engendre une déformation de la surface. Cette déformation est de forme sinusoïdale et fait apparaître un phénomène de compression au niveau de la surface.
C'est un phénomène qui est propre à la propagation d'une onde physique.
Fig. 11: [
Exemple de compression]Exemple de compression dans le cas d'une seule onde.
3.5.3 Position de repos de la surface
Étant donné sa nature même (une oscillation horizontale et une verticale), la paramétrisation classique donné par z=f(x,y) n'est pas possible.
En raison de la faible amplitude théorique des oscillations des particules fluides, nous allons considérer la surface comme paramétrée par sa position au repos. La surface est alors constituée par un maillage dont les sommets sont les centres des particules. Il s'agit en réalité de la surface horizontale de la mer au repos. Nous avons alors z0 = 0.
Nous retrouvons ici les équations
3.6 Représentation des ondes
Une composante relativement importante de la modélisation physique de la mer est la génération de l'ensemble des vagues que l'on va utiliser.
L'état de la mer est la résultante d'une superposition d'ondes de longueurs et périodes différentes engendrées par le vent. En dehors de la zone où souffle le vent, ces ondes se nomment la houle.
Nous allons donc représenter nos vagues par un ensemble d'ondes définies uniquement par leurs vecteurs d'ondes.
3.6.1 Vecteur d'onde
On défini pour chaque onde :
-
Son amplitude A
- Sa fréquence ω/2π
- Sa direction k/∥k∥.
Une génération automatique de ces différentes ondes existent [Thon et al. 2000] afin d'obtenir un spectre de référence. Dans notre cas, nous les avons simplement implémentés manuellement.
3.6.2 Relation de dispersion
Nous avons vu que le phénomène physique se ramène à la représentation du mouvement oscillatoire entre deux fluides. Nous avons vu que ce phénomène était dispersif.
Nous allons utiliser deux régimes distincts d'ondes: les ondes gravitationnelles et les ondes capillaires. On différencie les 2 régimes par la longueur de l'onde.
-
Pour des ondes avec λ > 1.7 cm: onde gravitationnelle
- Pour des ondes avec λ < 1.7 cm: onde capillaire
À l'intérieur du fetch (distance en mer sur laquelle souffle un vent donné sans rencontrer d'obstacle) sont générés un grand nombre de longueurs d'ondes différentes, parmi lesquelles certaines ont une durée de vie très limitée. Comme nous représentons le phénomène de houle, nous représentons les ondes en dehors de la zone de fetch.
Les pertes énergétiques engendrées par les déferlements et l'amortissement (viscosité des petites longueurs d'ondes) entraînent que seule une certaine gamme de fréquences est présente à l'extérieur du fetch. Ce sont les longueurs d'ondes les plus énergétiques qui vont se propager loin du fetch donc généralement, ce sont celles que l'on va vouloir représenter.
Cette amplitude est théoriquement définie par une étude fréquentielle [18]. De plus celle-ci peut être réalisée rapidement à l'aide d'un GPU comme présenté en [19].
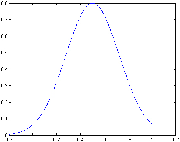
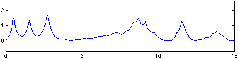
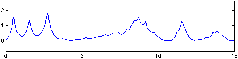
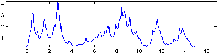
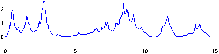
Nous avons donc représenté l'amplitude des vagues de façon simplifié par une Gaussienne centrée sur la pulsation de l'onde porteuse du phénomène de houle.
Fig. 12: [
Gaussienne utilisée]Gaussienne utilisée pour une onde porteuse de pulsation 0.5.
3.6.4 Etude des phénomènes liés à la profondeur
Nous avons décidé de rajouter à notre modèle la prise en compte du fond marin afin de modéliser aussi bien la houle en grand fond mais aussi à l'approche des plages.
La notion d'eau profonde ou peu profonde s'attache la plupart du temps au rapport entre la profondeur et la longueur de l'onde:
Pour prendre en compte ce paramètre, on utilise le modèle de houle de Airy. Nous redéfinissons la relation de dispersion afin de prendre en compte la profondeur
|
ω=√ |
|
⎛
⎜
⎜
⎝ |
g∥k∥+ |
|
⎞
⎟
⎟
⎠ |
tanh(∥k∥ h) |
|
|
-
Eau profonde
En eau profonde le terme tanh(∥k∥h) tend vers 1
On retrouve alors les 2 régimes d'ondes gravitationnelles et capillaires.
- Eau peu profonde (approche des plages)
Les ondes conservent leur pulsation ω et le vecteur d'onde k obéit alors à la loi de dispersion.
-
La longueur d'onde diminue, les vagues se rapprochent les unes des autres. C'est un phénomène de réfraction. Ce phénomène de réfraction entraîne une déformation du front d'onde à l'approche des plages.
- Enfin si l'amplitude est suffisante, la variation du vecteur d'onde entraîne un déphasage spatial progressif entre la crête et le creux de la vague. C'est ce qui fait que les vagues se penchent en avant à l'approche de la plage.
Fig. 13: [
Illustration du déphasage spatial]Illustration du déphasage spatial. Evolution des vecteurs d'ondes des crêtes et des creux des vagues pour illustrer el phénomène de déferlement
En prenant en compte la profondeur, on fait apparaître des limites à la représentation du modèle physique.
Le déphasage spatial est limité par le rapport entre l'amplitude et le vecteur d'onde. Une fois cette limite passée, le déferlement de la vague apparaît, ce qui se traduit par une perte d'énergie de l'onde.
Le modèle est aussi limité car il ne peux pas prendre en compte des profondeurs inférieures à la longueur d'onde.
3.7 Visualisation
Maintenant que nous avons défini notre modèle, il faut le représenter. Pour une approche temps réel, il est difficile de modéliser la surface autrement que sous la forme d'un maillage.
Fig. 14: [
Représentation du maillage triangulaire.]Représentation du maillage triangulaire utilisé pour notre modèle.
L'aspect de l'océan tient à sa composition d'un grand nombre d'ondes de directions et longueurs différentes.
Nous allons donc étudier comment nous pouvons réaliser le rendu de la surface de la mer sur un maillage pour un affichage temps réel.
Le rendu de la mer pose un certain nombre de problèmes. Dans une approche temps réel, il est très difficile de gérer la complexité nécessaire pour rendre compte fidèlement de toutes les perturbations de la surface qui lui donnent cet aspect si particulier.
Fig. 15: [
Reflexion à la surface de la mer]Photo de la réflexion sur la surface de la mer (tiré de [13])
Le comportement optique des surfaces liquides calmes, est suffisamment bien connu pour permettre une étude précise. Les surfaces liquides sont des réflecteurs presque parfaitement spéculaires. L'aspect primordial de la surface de la mer est donc la réflexion spéculaire.
3.7.1 La réflexion spéculaire
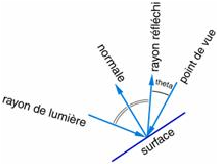
Le modèle de réflexion spéculaire se différencie du modèle de diffusion en faisant intervenir le point d'observation. Dans ce modèle les rayons de lumière sont réfléchis par symétrie par rapport à la normale de la surface. Il faut donc calculer quel est le rayon réfléchi sur la surface.
L'intensité de la lumière observée dépend de θ qui correspond à l'angle entre le rayon réfléchi et le point d'observation, de l'intensité Il de la source de lumière et du coefficient de réflexion ps de la lumière spéculaire (0 <= ps <= 1). Lorsque le rayon réfléchi arrive directement dans l'oeil, l'intensité est alors maximum.
Is=ps Il cos(θ)
Fig. 16: [
Calcul de l'effet spéculaire]Schéma représentatif de la direction des vecteurs pour la représentation de l'effet spéculaire
Il nous faut donc calculer les normales à notre surface pour représenter au mieux l'effet spéculaire. Comme les équations de la surface sont parfaitement connues, on peut calculer la normale de la surface.
On commence par calculer les dérivées à la surface dans les 2 directions du plan.
|
|
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩ |
|
|
|
|
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩ |
| nx=− |
|
Ai kix sin(ωi t−ki⋅ r0)) |
|
| |
| ny=− |
|
Ai kiy sin(ωi t−ki⋅ r0) |
|
| |
| nz=1− |
|
Ai2 |
|
cos(ωi t−ki⋅ r |
0)2 − |
|
Ai2 |
|
cos(ωi t−ki⋅ r0)2 |
|
| |
|
|
Fig. 17: [
Affichage avec texture.]Affichage des normales et de la texture.
Nous mettons ici uniquement en place l'aspect diffu et spéculaire de base d'OpenGL, cependant, des modèles plus complets d'illuminations sont présentés par exemple dans [20].
Nous avons réalisé notre modèle en intégrant différents paramètres réglables afin de les faire varier au cours du temps et observer les changements occasionnés sur le modèle.
-
Le nombre d'onde
On peut modifier le nombre d'onde prise en compte dans la superposition.
Fig. 18: [
Variation du nombre d'onde.]Variation du nombre d'onde. Une seule onde pour la première image et une composition de dix ondes pour les deux dernières images.
- L'effet spéculaire
Fig. 19: [
Effet spéculaire.]La première image montre l'affichage des normales qui vont servir à calculer l'effet spéculaire. La seconde est l'affichage du résultat du rendu.
- Orientation et profondeur du fond marin
On peut modifier la disposition du fond marin afin de représenter la mer soit en eau profonde soit à l'approche des plages. On peut ainsi modifier la profondeur et l'inclinaison du fond.
Fig. 20: [
]Les deux premières images montrent l'effet de la variation de la profondeur (2 m et 8 m). La dernière image montre le cas du sol incliné.
- Limite du modèle
Le modèle ne peut évidement pas modéliser les brisures de vagues. On observe alors un effet de recouvrement sur la représentation des vagues.
Fig. 21: [
Limitation du modèle]Limitation du modèle. Visualisation de l'effet de recouvrement du à la profondeur trop faible et amplitude des vagues trop grande.
4 Utilisation du Bruit de Perlin
COMPILE THIS:
main(k){float i,j,r,x,y=-16;while(puts(""),y++<15)for(x
=0;x++<84;putchar(" .:-;!/>)|&IH%*#"[k&15]))for(i=k=r=0;
j=r*r-i*i-2+x/25,i=2*r*i+y/10,j*j+i*i<11&&k++<111;r=j);}
Ken Perlin — http://mrl.nyu.edu/ perlin/
3DANS
cette partie, nous allons cette fois oublier l'aspect physique de la modélisation. On va maintenant s'intéresser à modéliser l'apparence des vagues par des fonctions de types bruits. En effet, il est bien connu que beaucoup de phénomènes peuvent se représenter par des fonctions aléatoires qui généralement ont en plus des propriétés fractales.
Cette fois c'est spécifiquement l'aspect visualisation qui est pris en compte. En effet, la théorie permettant de réaliser le lien entre la physique et la fonction fractale n'est généralement pas connue. C'est donc le plus souvent par des approches ad-hoc que se réalisent certaines représentations. Néanmoins, l'aspect donné par certains bruits sont d'un réalisme surprenant.
4.1 But de la méthode
Afin de réaliser des vagues, nous allons tout d'abord considérer une surface plate. Celle-ci peut être définie par exemple par un plan comme nous l'avons illustré dans le chapitre précédant.
Cette surface va être déformée, cependant, cette fois la fonction de déformation ne va pas être explicitement connue. Dans le cas précédant, l'expression de la fonction sous forme de sinus pouvait générer des effets de répétitions et était évidemment limitée au niveau de l'aspect réaliste par la complexité de celle-ci.
Dans le but d'éviter ces effets indésirables tout en gardant une complexité faible de la fonction de déformation, nous allons utiliser un bruit particulier: le bruit de Perlin. Une fois ce bruit calculé, nous allons simplement déformer la surface suivant la valeur renvoyée par ce bruit au point consideré. Un type de bruit correctement paramétré et de nature fractale va alors pouvoir modéliser les différentes échelles présentes à la surface de l'eau ainsi que les crètes raides de certaines vagues. Modélisation qui est complexe à réaliser à partir de fonctions sinusoïdales.
4.2 Bruit de Perlin
Ce type de bruit est la base de très nombreuses applications dans le domaine de la visualisation. Initialement introduit par Ken Perlin en 1989 [21] ce bruit est devenu depuis l'une des fonction fondamentale de la synthèse de textures et surfaces diverses (tel que la créatio de montagnes).
Pour introduire ce bruit, supposons tout d'abord que l'on recherche simplement à construire la surface d'une colline.
Les fonctions de types cosinus peuvent permettre d'approcher l'aspect du terrain, cependant celle-ci sont très répétitives et nécessite de nombreuses sommations bien paramétrées afin de donner une allure aléatoire réaliste.
Dans l'autre cas, l'utilisation de simples fonctions aléatoires (type rand() ) ne permet par de donner un aspect correct, car à chaque nouvelle position, une valeur indépendante de la précédante est choisie. La fonction ainsi obtenue n'est alors évidement pas continue.
On recherche donc une fonction continue en x ayant des propriétés d'amplitudes aléatoires.
Dans le cas 1D, on considère un ensemble de valeurs k0 tel que k0=f(n) avec n∈N. Les valeurs de k0 sont donc renvoyées pour un paramètre entier n. On ne connaît pas la fonction f et celle-ci peut être de type aléatoire (mais renvoie la même valeur à n fixé). On considère que f renvoie une valeur entre 0 et 1. Généralement, la nature de ce bruit sera de type uniforme3.
Ken Perlin dénote cette fonction f par le terme de pseudo aléatoire, car les valeurs revoyées ne sont pas connues à l'avance, par contre celle-ci sont toujours les même lorsque la variable n est la même.
Par exemple, la fonction f=mod(100000 n+112312 n2,M)/M, avec M grand4 pourrait tout à fait convenir pour construire ce type de fonction. On recherchera également des méthodes de calculs rapides en fonction de n. Les méthodes les plus rapides stockant généralement ces valeurs dans des vecteurs précalculés, puis utilisent des tables de hachages pour y accéder de façon aléatoire.
Ces valeurs k0 vont maintenant nous servir de points de contrôle pour la fonction définie. On considère en effet maitenant x quelconque dans R. La valeur de la fonction pseudo-aléatoire en un point x va simplement être donnée par interpolation entre les valeurs de k0. Cette méthode permet donc d'obtenir une fonction continue en x mais dont les valeurs restent aléatoires.
Appelons γ la fonction ainsi définie.
Un exemple de construction est ainsi montré en fig. 22
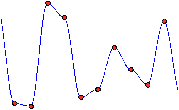
Fig. 22: [
Construction du bruit de perlin par interpolation.]Construction de la fonction γ du bruit de perlin par interpolation de positions aléatoires. La première figure montre les points rouges correspondants aux valeurs de k0 alors que la seconde figure montre γ interpolant ces valeurs.
La fonction définie ici dans le cas monodimentionnel se généralise de façon immédiate au cas multidimentionnel en notant cette fois γ(x)=γ∘ u (x), avec x∈RN et u une fonction de RN dans R permettant de “mélanger” les coordonnées entre elles. On peut simplement prendre u comme une forme linéaire dont les coefficients sont suffisamment importants pour empêcher toute corrélation entre les axes.
Exemple: u(x)=Σi ai xi et les ai sont choisis tels que a1=1 et ai=100 ai−1 afin d'éviter toute corrélation du type γ(Σi ai xi)=γ(b), pour b∈R.
On dispose ainsi de la fonction γ:RN→ [0,1] qui sera notamment utile pour N=3. Un exemple est présenté en fig. 23.
Fig. 23: [
Bruit de Perlin simple en deux dimensions.]Bruit de Perlin simple pour le cas à deux dimensions.
Il est de même évident de construire une fonction vectorielle à partir de cette définition. Ken Perlin préconise ainsi pour une fonction vectorielle dans Cm (où cette écriture correspond au cube unité défini par l'espace Cm = Πi=1m [0,1]) la définition suivante: γi(x) = γ(x+σ), où ∥σ∥ est pris suffisament grand pour éviter toute corélation entre les valeurs.
On peut ainsi appliquer ce cas à la création de textures colorées comme le montre la fig. 24.
Fig. 24: [
Bruit de Perlin simple en deux dimensions en couleur.]Bruit de Perlin simple pour le cas à deux dimensions à valeurs vectorielles. Ici la sortie est codée en rouge, vert et bleu.
Nous avons donc à notre disposition (sans réel surcoût de complexité) la fonction
que nous utiliserons généralement dans l'espace 3D.
4.2.2 Interpolation
Nous avons simplement mentionné que l'opération nécessitait l'interpolation de la valeur au point x. Les choix des fonctions d'interpolations sont nombreux, nous rapellons brièvement les interpolations de bases.
- Interpolation Linéaire
Le cas le plus simple consistant en l'interpolation linéaire (et bi/tri linéraire en deux puis trois dimensions) est simplement donné par
f(u) = u f(0)+(1−u)f(1)
,
où u est la variable normalisée telle que u=x−⌊ x ⌋/⌈ x ⌉ − ⌊ x ⌋, avec ⌊ ⌋, l'opérateur floor (entier inférieur le plus proche) et ⌈ ⌉ l'opérateur ceil (entier supérieur le plus proche). Évidemment, lorsque le vecteur des points est disposé de façon uniforme sur Z, le dénominateur ⌈ x ⌉ − ⌊ x ⌋ est constant et se simplifie pour donner 1.
En notant I l'opérateur d'interpolation défini ainsi, on peut exprimer l'interpolation bilinéraire:
f(u,v) = I(f(u,0),f(u,1))
,
où l'on voit que l'on réduit l'interpolation en dimension 2 à deux interpolation suivant la première dimension puis une suivant la seconde.
La méthode peut se mettre aisément sous forme récursive par
|
f(u)=I(f[ |
⎛
⎝ |
(ui)i∈[1,N−1],0 |
⎞
⎠ |
,f |
⎛
⎝ |
(ui)i∈[1,N−1],1 |
⎞
⎠ |
])
,
|
- Interpolation Cubique
Le point négatif de l'interpolation linéraire est que celle-ci donne un aspect triangulaire en dimension 2 ou supérieure. On peut ainsi mentionner un autre interpolation également très répendue : l'interpolation cubique (avec ces généralisations bi/tricubique). Celle çi peut s'exprimer avec la formule d'interpolation de Lagrange [22]. L'interpolation est cette fois meilleure que par une simple fonction linéaire, cependant l'algorithme est plus lourd à gérer car il nécessite la valeur de f des deux précédécésseurs et des deux successeurs5. Dans le cas de points régulièrement espacés par pas de 1, on note x0,x1,x2,x3 les points connus localement où x0=⌊ x−1⌋ et xi+1=xi+1.
On peut alors exprimer l'interpolation par
|
|
| f(x) = |
(f(x3)−f(x2)+f(x1)−f(x0)) |
u3 |
| |
+(−f(x3)+f(x2)−2 f(x1)+ 2 f(x0)) |
u2 |
| |
+(f(x2)−f(x0)) |
u |
| |
+f(x1) |
|
.
|
- Interpolation Sinusoïdale
Une méthode intermédiare peut également être considérée en utilisant la fonction de base de forme sinusoidale ϕ(u)=1/2(1−cos(π u)). Cette fois, on peut approximer l'allure d'un polynome d'ordre >1 en utilisant uniquement les deux plus proches voisins6 avec la relation
f(x) = ϕ(x) f(0)+(1−ϕ(x)) f(1)
.
- Interpolation Splines
D'autres méthodes permettent d'obtenir des courbes encore plus lisses. On citera ainsi les Splines (notamment celles d'ordres 3) permettant d'obtenir des courbes C2 [23].
Le temps de calcul est globalement le même que pour l'interpolation cubique mais celle-ci possèdent des propriétés encore plus interessantes aux niveaux des raccords. Nous pourrions implémenter cette méthode, cependant ce rapport ne se spécialise pas dans la mise au point optimale du bruit de Perlin, et la méthode cubique étant déjà suffisement lente lors de l'implémentation, nous laissons la mise en place de l'interpolation spline pour une amélioration future possible.
Une comparaison entre les méthodes d'interpolations linéaires basées sur un sinus et interpolations cubique est réalisée en fig. 25.
On note ici le code c utilisé pour construire l'interpolation.
L'interpolation linéaire est réalisée par la fonction
double interpolate_1D_linear(double v0,double v1,double x)
res = v1*(1-x)+v2*x;
Celle sinusoïdale par
double interpolate_1D_sinus(double a,double b,double x)
double f=(1-cos(ft*PI))*0.5;
res = a*(1-f)+b*f;
alors que l'interpolation cubique est réalisée par:
double interpolate_1D_cubic(double v0,double v1,double v2,double v3,double x)
res = v1+x*((v2-v0)+x*((-v3+v2-2*v1+2*v0)+x*(v3-v2+v1-v0)));
L'enchainement de l'interpolation pour le cas tricubic nécessite un nombre important de calcul (concernant le nombre d'appel à la fonction f) et la méthode utilisée est rappelée ici pour le cas 3D:
%tableau des positions et des interpolations
double V[64];double Ix[16];double Ixy[4];
%valeurs au sommet
for(k3=0:4)
for(k2=0:4)
for(k1=0:4)
V[k1+4*(k2+4*k3)] = noise_3D(int_x+k1-1,int_y+k2-1,int_z+k3-1);
%interpolation en x
for(k3=0:4)
for(k2=0:4)
k=k2+4*k3;
Ix[k] = interpolate_1D_cubic(V[4*k+0],V[4*k+1],V[4*k+2],V[4*k+3],frac_x);
%interpolation en y
for(k3=0:4)
Ixy[k3] = interpolate_1D_cubic(Ix[4*k3+0],Ix[4*k3+1],Ix[4*k3+2],Ix[4*k3+3],frac_y);
%interpolation en z
return interpolate_1D_cubic(Ixy[0],Ixy[1],Ixy[2],Ixy[3],frac_z);
Fig. 25: [
Comparaison des méthodes d'interpolations.]Comparaison des méthodes d'interpolations. La première colonne concerne l'interpolation pour le cas 1D alors que la seconde colonne concerne le cas 2D. Les lignes correspondent aux méthodes d'interpolations. La première ligne est celle réalisée par l'interpolation linéaire, la seconde est celle réalisée par interpolation sinusoïdale, alors que la dernière correspond à l'interpolation cubique.
L'interpolation linéaire s'avère visiblement être assez peu utilisable car l'anisotropie est très importante et la surface n'est pas lisse aux jointures. Le cas de l'interpolation sinusoïdale parrait un bon compromis entre la simplicité et la rapidité (à condition de précalculer une table (Look Up Table) pour la fonction de base en cosinus). Par contre, si cela ne se voit pas sur des images, cette méthode possède l'inconvénient de se détecter lors d'une animation (notamment à cause de la tangente nulle à chaque valeur entière. Les vagues varient alors linéairement pendant un moment puis semblent stagner et enfin reprennent leur rythmes. Cela donne une impression peu réaliste.).
L'interpolation cubique donne les meilleurs résultats mais est plus lente car celle-ci nécessite le calcul de 16 fois plus de valeurs en 3D pour chaque position7. La méthode s'avère cependant très bonne pour le cas de l'animation (la tangente n'est plus forcément nulle à chaque entier).
4.2.3 Mise en place de l'aspect fractal.
Nous avions annoncé que le bruit devait avoir une nature fractale. Celui présenté jusqu'à présent est cependant complètement lisse (sauf en un nombre fini de points si l'on prend des interpolations d'ordre 0 ou 1).
La mise en place de l'aspect fractal va maintenant se réaliser simplement par une construction itérative de la fonction. Pour cela, on va juste sommer le bruit ainsi créé avec des fréquences de plus en plus élevés et des amplitudes de plus en plus faibles.
La fonction fractale générale associée au bruit de perlin va alors être notée
où γ et γ∞ sont des fonctions de RN vers Rm.
Le paramètre a va donc correspondre à l'augmentation de la fréquence à chaque niveau d'échelle. Ce paramètre est généralement pris égal à 2 dans les implémentations standards.
Le paramètre b correspond à celui de réduction d'amplitude. Plus celui-ci est faible, plus les hautes fréquences vont avoir des amplitudes importantes et donc persister pour plusieurs échelles. Pour cela, le terme 1/b est souvent appelé persistence.
La convergence est assurée dès lors que |b|>1. En effet, on pourra remarquer que l'on avait posé que ∥γ∥∞≤ 1, donc8
en reconnaissant la somme de la série géométrique Σk b−k.
Évidemment, cette somme infinie n'est pas implémentable directement. On tronque donc le nombre d'itérations à une valeur p maximale. Cette valeur est généralement appelée le nombre d'octaves. La fonction ainsi définie est alors
La valeur du nombre d'octaves permet donc d'un autre coté de limiter l'aspect fractal de la surface. En ne considérant qu'un faible nombre d'itérations. D'un autre coté, si l'on souhaite obtenir une surface très accidentée, ce paramètre va être choisi de façon suffisament importante pour que les paramètres tronqués ne soient de toute façon pas visibles lors de l'affichage.
On notera qu'une fois de plus, on peut connaitre les bornes maximales de la fonction. Cela permet de limiter par la suite son amplitude si nécessaire (notamment pour les cas des couleurs où l'on souhaite obtenir des valeurs sur chaque composante comprise entre 0 et 1).
Dans le cas de la somme partielle, on obtient par la même méthode de suite géométrique
Enfin, on remarquera également que si l'interpolation le permet, la fonction est dérivable et la dérivé peut être donnée explicitement ce qui peut être avantageux lors d'une implémentation9.
Par linéarité de la dérivation sur la somme partielle, on obtient donc
Cette formule n'est évidement valable que si γ est dérivable elle même (problèmes avec les interpolations d'ordre 0 et 1 pour un nombre de points tendant vers l'infini à mesure que p augmente.).
Finalement, on peut faire remarquer que si l'on utilise la formule donnée de cette façon, lors du passage d'un octave à l'autre, on va répéter le motif précédant sur une partie de l'octave suivant. En effet, en prenant le cas 2D et une augmentation d'échelle par un facteur a=2, la première moitié de la figure de l'échelle k+1 consiste en celle de l'echelle k. Pour éviter une répétition de motif visible, on peut réaliser une “réinitialisation” du bruit pour chaque échelle. On peut réaliser cela facilement en translatant par un nombre suffisament important les coordonnées à chaque échelle. L'expression du bruit devient alors
où ∥Ak∥ est suffisamment important et variant à chaque échelle.
La méthode de sommation d'un nombre fini d'octaves est montré en fig. 26 et devrait être suffisamment explicite pour comprendre le principe de la construction du bruit par sa simple observation.
Fig. 26: [
Construction itérative du bruit de Perlin.]Schéma de la construction itérative du bruit de perlin par sommation de fréquence croissante et d'amplitude décroissante. La colonne de gauche montre le cas 1D alors que celle de droite montre le cas 2D.
4.2.4 Application aux textures
Nous montrons ici une fonction de bruit utilisée. Les nombres choisis ne sont absolument pas significatifs et d'autres pourraient parfaitement convenir (on notera la présence de la variable Ak étant une variable globale réalisant la translation lors du changement d'échelle)
static double noise_3D(int x,int y,int z)
{
res = 413243*(x<<12+234123*(x<<10)+(y<<6)*31412
+(z<<12)*13243+54235239*(x*23+y*3142-z*432
+x*y*54324-z*x*4312))+120+43124132*y
+4321432*z-41231*x+Ak;
res = fabs(res);
res = ((int)res)%1000000/(float)1000000;
return res;
}
Une fonction c est notamment implémentée sous forme de fichier mex sous Matlab pour un calcul rapide dans le cas 3D.
Les applications du bruit de Perlin sont très nombreuses.
On peut premièrement penser évidememnt à la création de textures avec le cas 2D en niveau de gris ou en couleur. Un exemple est montré en fig. 27. On pourra remarquer que ces textures sont typiquements celles fournies par le logiciel gimp sous la dénomination de “rendu de nuage”.
Fig. 27: [
Exemple de textures créé par un bruit de perlin.]Exemple de texture 2D créés de façon aléatoire par un bruit de perlin. La figure de gauche montre le cas à niveaux de gris alors que celle de droite montre le cas en couleurs.
Il est d'ailleur facile de créer des textures donnant l'impression de nuages afin de texturer un ciel en jouant sur la couleur.
Ainsi le script matlab suivant:
P0 = get_perlin_noise(xx,yy,zz,5,1/2,2,0);
P0 = 1-min(2*P0,1);
pic = zeros([size(P0),3]);
pic(:,:,1)=P0*0.6+0.4;
pic(:,:,2)=P0*0.6+0.4;
pic(:,:,3)=P0*0.2+0.8;
imagesc(u,u,pic);
axis square
donne la texture montré en fig. 28.
Fig. 28: [
Texture de nuages par bruit de Perlin]Exemple de texture de nuages générée par le bruit de Perlin. La figure de gauche correspond à une texture générée automatiquement. La figure de droite représente celle d'un vrai ciel légèrement nuageux prise par un appareil numérique le 28/01/2007.
Il est possible d'envisager toute une panoplie d'autres types de textures.
On peut ainsi facilement créer des textures de type marbre par des fonctions du type cos(a⋅ x+b γ(x)). On applique ainsi une texture de ce type sur une sphère sous Matlab pour obtenir la fig. 29.
Le code de la texture est donné par:
noise = (get_perlin_noise(xx,yy,zz,7,1/1.8,2,0)-0.5)*2;
noise = (cos(8*(x+y+0.25*noise)*pi)+1)/2;
for(k=1:3)
pic(:,:,k) = noise;
surf(xx,yy,zz,'CData',pic,'EdgeColor','none');
On peut également obtenir rapidement une texture de type bois en considérant cette fois γ(x)−⌊ γ(x) ⌋. un exemple de code Matlab est donné par
noise = 9*get_perlin_noise(xx*1.5,yy*1.5,zz*1.5,2,1/2.5,2,0);
noise = noise-round(noise);
Il suffit de faire évoluer la couleur entre 2 tons de marrons pour obtenir une impression de bois comme le montre la fig. 29.
Enfin, on peut obtenir également simplement des textures donnant l'impression de flammes. Le code suivant permet de réaliser cette effet
base = 1-abs(2-x)/Xmax+y.*sin(x/Xmax*pi)/Xmax;
noise = 1.5*U+get_perlin_noise(xx*1.5,yy*1.5,zz*1.5,5,1/2,2,0);
noise = max(2*noise,1);
imagesc(noise);
colormap hot(256);
Fig. 29: [
Type de textures créés par le bruit de Perlin.]Différents types de textures pouvant être créés rapidement par un bruit de Perlin. De gauche à droite sont représentées les imitations de marbre, bois et flamme.
Cette liste est loin d'être exaustive, mais nous nous limiterons à ces exemples dans le cadre de ce rapport.
4.2.5 Application au déplacement
Afin de donner l'impression d'eau, il faut cette fois déplacer physiquement les vertex pour leur donner un relief.
- La première façon de réaliser ce déplacement est évidement de considérer une grille de vertex paramétrés par (x,y), intialement construite avec z=0.
En affectant z=γp(x,y), on obtient alors un déplacement continu et aléatoire de la surface qui va pouvoir modéliser la forme des vagues.
Cette méthode va être implémentée sous OpenGL afin d'obtenir un déplacement en temps réel dans la partie suivante.
- Une seconde façon de réaliser ce déplacement correspond à la perturbation d'une isosurface.
Cette méthode est très puissante pour déformer tout type de surface. Pour cela on se place dans le cas 3D et on considère une fonction ϕ:R3→R telle qu'une isosurface soit définie de facon implicite par:
{ x∈R3 | ϕ(x)=0
}
Cette isosurface va alors définir un ou plusieur objets. Dans le cas de fonctions simples, ces objets seront généralement lisses pour peu que ϕ soit continue. Il va alors être possible de leur donner un aspect plus naturel en ajoutant une fonction de bruit en recherchant la nouvelle isosurface telle que par exemple:
{ x∈R3 | ϕ(x)+γp(x)=0
}
La puissance de cette représentation est qu'elle est indépendante de la topologie de l'objet. Ainsi la surface de l'eau déformée ne sera pas contrainte à être topologiquement liée à un plan mais pourra posséder des ensembles non connexes pouvant modéliser des gouttes d'eau projetées par exemple.
Différentes méthodes permettent de tracer des isosurfaces efficacement et de les mailler pour une représentation sous OpenGL, notamment l'algorithme bien connu du “marching cube” [24]. Dans notre cas, nous utiliserons directement l'isosurface rendu par une méthode de ray-tracing permettant de gérer facilement le problème de sa visualisation.
Prenons par exemple le cas du plan. Celui çi peut être délimité en prenant la fonction ϕ(x,y,z)=z. Nous obtenons alors dans ce cas la surface correspondant au plan z=0. L'ajout d'un bruit de Perlin sur cette fonction ϕ+γp va alors déformer le plan et l'isosurface correspondante ne sera plus un plan parfait.
Des exemples sur un plan et sur une sphère implémentés sous Matlab sont montrés en fig. 30
Fig. 30: [
Déformation d'isosurfaces.]Images des déformations de la fonction implicite par un bruit de Perlin. Les figures de gauche montrent les isosurfaces non bruitées alors que les figures de droite montrent celles obtenues après l'application du bruit.
Le code Matlab complet de la déformation de la sphère est le suivant:
N=20;
u=linspace(-1,1,N);
[xx,yy,zz]=meshgrid(u,u,u);
A=0.2;R=0.6;
%noise
noise = get_perlin_noise(3*xx,3*yy,3*zz,3,1/2,2,0);
%function
phi = xx.^2+yy.^2+zz.^2-R.^2+A*noise;
%draw
p = patch(isosurface(xx,yy,zz,phi,0));
isonormals(xx,yy,zz,phi,p);
set(p,'FaceColor','blue','EdgeColor','none');
camlight;
lighting phong;
material shiny;
axis equal
axis([-1,1,-1,1]);
axis vis3d
view([95,35]);
set(gca,'color','white','xtick',[],'ytick',[],'ztick',[]);
set(gcf,'color','white');
Cette méthode sera utilisée dans la dernière partie du rapport concernant le rendu par ray-tracing.
Le bruit de Perlin:
-
Permet de modéliser un bruit continu et de nature fractale.
- On contrôle le nombre d'itérations et de changements d'échelles pour donner un aspect plus ou moins accidenté.
- S'applique sans aucune difficultée au cas 3D scalaire ou vectoriel.
- Nécessite un choix d'interpolation (l'interpolation cubique donne de bons résultats).
- Permet de modéliser de nombreux phénomènes sous forme de textures.
- Permet de réaliser des déformations pour donner un aspet physique: déformation de la position des vertex ou déformation d'une fonction 3D définissant une isosurface.
4.3 Implémentation sous OpenGL
On va, dans cette partie, s'interresser spécifiquement à l'implémentation de ce bruit sous OpenGL.
4.3.1 Mise en place des classes de gestion des surfaces
Une classe d'affichage de la surface d'eau est implémentée. Comme celle-ci sera définie sous la forme d'une surface paramétrique (x(u,v),y(u,v),z(u,v)), on implémente une classe permettant de gérer facilement ce type de surface.
La classe Parameterized surface va gérer cette surface paramétrique en stockant dans des tableaux les vertex, normales, coordonnées de textures, couleur et connectivité.
Son prototype est le suivant:
class Parameterized_surface
{
public:
Parameterized_surface();
~Parameterized_surface();
//init
int set_size(int N_1,int N_2);
int set_properties(int is_normal,int is_texture_coordinate,int is_color);
int set_flat_surface(float L1_min,float L1_max,float L2_min,float L2_max);
//set
int set_x3(int k1,int k2,float value);
int set_vertex(int k_1,int k_2,float x,float y,float z);
int set_color(int k_1,int k_2,float r,float g,float b);
int set_color(int k_1,int k_2,float r,float g,float b,float a);
int fill_x3(float value);
int scale(float s_x,float s_y,float s_z);
//texture
int map_environmental_texture(float H,float s_1,float s_2);
//normal
int update_normal();
int calculate_dimensions();
float *get_dimensions();
int normalize_x3(float min_x3,float max_x3);
float get_x(int k_1,int k_2);
float get_y(int k_1,int k_2);
float get_z(int k_1,int k_2);
int get_N_vertex();
int get_N_connectivity();
float *get_vertex();
float *get_normal();
float *get_color();
float *get_texture_coordinate();
unsigned int *get_connectivity();
private:
int destroy();
int alloc();
int build_connectivity();
int fill_flat_surface();
int N_1,N_2;
int N_vertex,N_connectivity;
int N_color,N_texture;
float dimensions[6];
float *vertex;
float *normal;
float *texture_coordinate;
float *color;
unsigned int *connectivity;
int is_normal,is_texture_coordinate,is_color;
};
La classe s'occupe des tâches fastidieuses de la constuction de la connectivité et de la gestion des tailles.
Le calcul des normales est réalisé par une fonction encore plus bas niveau ne traitant que les vertex de topologie arbitraire. Cette classe Mesh Tool
class Mesh_tool
{
public:
Mesh_tool();
~Mesh_tool();
int scale(float s_x,float s_y,float s_z,int N_vertex,float *vertex);
int get_normal(int N_connectivity,unsigned int *connectivity,
int N_vertex,float *vertex,float *normal);
private:
};
va calculer les normales par différences finies entre les vertexs d'un triangle. Puis, pour chaque vertex, on moyenne la normale pour l'ensemble des triangles dont le vertex considéré fait partie.
Ces classes ne seront cependant pas plus détaillées ici car ce n'est pas l'objet de ce rapport.
L'ensemble des vertex sont repris dans une classe plus globale Water surface
class Water_surface
{
public:
Water_surface();
~Water_surface();
int set_size(int N_x,int N_y,float min_x,float max_x,
float min_y,float max_y,float min_z,float max_z);
int draw();
int update_water(int kt);
int scale(float s_x,float s_y,float s_z);
private:
int load_texture();
int N_x,N_y;
float dimensions[6];
Parameterized_surface surf;
GLuint texture_number;
};
permettant de gérer l'eau en affectant chaque vertex à une position. La classe s'occupe également du lien avec la partie OpenGL en effectuant l'affichage à l'aide des tableaux de sommets. La méthode draw est alors la suivante:
int Water_surface::draw()
{
GLfloat M_specular[3]={0.8,0.8,0.8};
GLfloat M_shiny = 130;
glMaterialfv(GL_FRONT,GL_SPECULAR,M_specular);
glMaterialf(GL_FRONT,GL_SHININESS,M_shiny);
glEnable(GL_LIGHTING);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D,texture_number);
glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_NORMAL_ARRAY);
glEnableClientState(GL_COLOR_ARRAY);
glEnableClientState(GL_TEXTURE_COORD_ARRAY);
%set position in memory
glVertexPointer(3,GL_FLOAT,0,surf.get_vertex());
glNormalPointer(GL_FLOAT,0,surf.get_normal());
glColorPointer(4,GL_FLOAT,0,surf.get_color());
glTexCoordPointer(2,GL_FLOAT,0,surf.get_texture_coordinate());
%draw
glDrawElements(GL_TRIANGLES,surf.get_N_connectivity(),
GL_UNSIGNED_INT,surf.get_connectivity());
glDisableClientState(GL_TEXTURE_COORD_ARRAY);
glDisableClientState(GL_NORMAL_ARRAY);
glDisableClientState(GL_VERTEX_ARRAY);
glDisableClientState(GL_COLOR_ARRAY);
glDisable(GL_TEXTURE_2D);
glDisable(GL_LIGHTING);
return 0;
}
On peut alors mettre en place rapidement une grille évoluant sous la forme sinusoïdale uniquement sur z (voir première partie du rapport sur l'aspect non physique de cette modélisation).
La mise en place de cette grille est montrée en fig. 31 qui nous servira de base pour rendre l'impression d'une petite rivière. Dans cette exemple, la mise en place de la grille se réalise simplement par l'appel à la méthode (dans la classe Water Surface)
surf.set_x3(k_x,k_y,z);
Fig. 31: [
Mise en place de la grille paramétrique en OpenGL]Mise en place de la grille Paramétrique en OpenGL
La mise en place des trochoïdes pourraient cependant ce réaliser sans aucune complexité supplémentaire.
4.3.2 Mise en place du Bruit de Perlin
Ensuite, nous mettons en place la classe de création du bruit de Perlin. Cette implémentation se réalise par la classe Perlin noise dont l'entête (limité au cas 3D ici pour gagner de l'espace) est la suivante:
class Perlin_noise
{
public:
float get_perlin(float x,float y,float z,int octave,float persistence,
float frequency);
private:
float interpolate_noise_3D(float x,float y,float z);
float interpolate_cubic_1D(float v0,float v1,float v2,float v3,float x);
float noise_3D(int n1,int n2,int n3);
};
Dans ce cas, l'interpolation cubique est utilisée. On rapelle que celle-ci donne de bien meilleurs résultats lors de l'animation par contre, on rapelle également qu'elle ralentie considérablement la rapidité de l'algorithme par un facteur 16.
Les fonctions de création sont globalement identiques à celles présentées pour le cas de Matlab et ne sont pas plus détaillées. Le résultat de l'appel suivant
z = 0.02*cos(6*x-ct/2)
+0.07*noise.get_perlin(x,y,Z0+ct/10,octave,persistence,frequency);
surf.set_x3(k_x,k_y,z);
est affiché en fig 32
Fig. 32: [
Mise en place du bruit de Perlin sur la grille.]Mise en place du bruit de Perlin sur la grille paramétrique.
L'aspect de mouvement global de la vague est ainsi donné par le sinus alors que la complexité des vaguelettes est donnée par le bruit. Pour éviter un effet de translation trop simple lors du mouvement, on fait évoluer le bruit de façon continue en modifiant l'offset du bruit sur z en rendant ce paramètre dépendant du temps.
Ce type de scène à été implémenté en [25] avec ces paramètres. Nous nous en sommes notamment inspirés pour la scène que nous allons mettre en place dans le paragraphe suivant.
4.3.3 Mise en place de la scène
Une scène d'aspect naturel peut alors être implémentée. Pour cela, la surface doit être texturée.
La transparence vraie n'est pas évidente à gérer car celle-ci nécessiterait de gérer le Z buffer manuellement. Or, on ne sait pas à priori quelle partie de la vague est située devant ou derrière nous. Une solution consisterait à trier à la main chaque vertex en profondeur par rapport à la position locale de la caméra, par contre le calcul couterait encore plus cher au niveau du temps de calcul.
Cependant, pour une hauteur de vague faible, on peut activer une transparence légère sans que le problème d'affichage due à la gestion de la profondeur soit trop visible.
La première étape consistant à donner une impression de relief de la vague va être réalisée en faisant dépendre la couleur de l'eau avec sa hauteur. En effet, on peut penser que plus une vague sera haute, plus les remous à son sommet et la faible épaisseur de l'eau vont lui donner un aspect blanc. Un exemple est ainsi montré en fig. 33
Fig. 33: [
Changement de coloration de la vague suivant la hauteur.]Changement de coloration de la vague suivant sa hauteur en z en lui donnant un dégradé entre le bleu et le blanc.
On peut également plaquer une texture donnant l'impression de remous sur la surface. On utilise dans notre cas un fond bleuté avec la texture affichée en fig. 34
Fig. 34: [
Texture d'eau utilisée.]Texture d'eau utilisée. Celle-ci est créée par Gimp à l'aide du bruit de Perlin.
Le plaquage direct peut être envisagé. On peut également translater ces mêmes coodonnées suivant le sens de la vague afin de donner l'impression de mouvement.
Cependant la texture parraît toujours statique et plaquée par rapport à la surface. Une méthode permet cependant d'améliorer nettement l'aspect de mouvement: la texture environnementale.
En effet, une partie de la coloration de l'eau dans la nature nous vient de la reflection du ciel. On peut alors supposer qu'en reflétant une texture de type nuageuse, on peut obtenir des résultats intéressants.
La méthode de la texture environnementale se réalise normalement par rapport à un cube texturé. Notre implémentation est réalisée sommairement en ne prennant en compte qu'un plan situé à une hauteur constante.
Le schéma correspondant à ce modèle est montré en fig. 35
Fig. 35: [
Schéma de la mise en place de la texture environnementale.]Schéma de la mise en place de la texture environnementale.
Dans le cas 2D, il suffit alors d'affecter pour le vertex (kx,ky) la coordonnée de texture
|
(u,v)=(x+(H−z) |
|
, y+(H−z) |
|
)
(18) |
Fig. 36: [
Exemple de texture sur la surface.]Exemple de texture plaquée sur la surface. L'image de gauche correspond au plaquage simple où les coordonnées de textures sont directement liées aux paramétrage de la surface. L'image de droite correspond à la mise en place de la texture environnementale donné en eq. 18.
On peut évidemment cummuler le meilleur des deux en utilisant le multitexturing appliqué sur la surface10.
Ainsi le code suivant fournit l'illustration donnée en fig. 37.
//enable multitexturing
glActiveTextureARB(GL_TEXTURE0_ARB);
glBindTexture(GL_TEXTURE_2D,texture_number);
glEnable(GL_TEXTURE_2D);
//multiply texture with color
glTexEnvf (GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_COMBINE_EXT);
glTexEnvf (GL_TEXTURE_ENV, GL_COMBINE_RGB_EXT, GL_MODULATE);
glClientActiveTextureARB(GL_TEXTURE0_ARB);
glTexCoordPointer(2,GL_FLOAT,0,&multitexturing[0]);
glEnableClientState(GL_TEXTURE_COORD_ARRAY);
glActiveTextureARB(GL_TEXTURE1_ARB);
glBindTexture(GL_TEXTURE_2D,texture_number);
glEnable(GL_TEXTURE_2D);
//then add the new one
glTexEnvf (GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_COMBINE_EXT);
glTexEnvf (GL_TEXTURE_ENV, GL_COMBINE_RGB_EXT, GL_ADD_SIGNED);
glClientActiveTextureARB(GL_TEXTURE1_ARB);
glTexCoordPointer(2,GL_FLOAT,0,&multitexturing[2*N_x*N_y]);
glEnableClientState(GL_TEXTURE_COORD_ARRAY);
glVertexPointer(3,GL_FLOAT,0,surf.get_vertex());
glNormalPointer(GL_FLOAT,0,surf.get_normal());
glColorPointer(4,GL_FLOAT,0,surf.get_color());
//draw
glDrawElements(GL_TRIANGLES,surf.get_N_connectivity(),
GL_UNSIGNED_INT,surf.get_connectivity());
glDisableClientState(GL_NORMAL_ARRAY);
glDisableClientState(GL_VERTEX_ARRAY);
glDisableClientState(GL_COLOR_ARRAY);
glActiveTextureARB(GL_TEXTURE1_ARB);
glClientActiveTextureARB(GL_TEXTURE1_ARB);
glDisableClientState(GL_TEXTURE_COORD_ARRAY);
glDisable(GL_TEXTURE_2D);
glActiveTextureARB(GL_TEXTURE0_ARB);
glClientActiveTextureARB(GL_TEXTURE0_ARB);
glDisableClientState(GL_TEXTURE_COORD_ARRAY);
glDisable(GL_TEXTURE_2D);
Fig. 37: [
Exemple de mutlitexturing.]Multitexturing appliqué sur l'image de l'eau. Une texture simple est plaquée par rapport aux coordonnées paramétriques de la surface et celle-ci est modulée par la texture environnementale. De plus on garde toujours une couleur plus claire pour les vagues les plus hautes.
Enfin, pour donner l'impression de rivière, on place un petit paysage entourant l'eau. Afin de donner une impression de relief naturel, on utilise le bruit de perlin afin de déplacer les vertex. Ce type de construction de terrain est assez généralement utilisé dans les logiciels de création de paysage (on pensera notamment à Terragen utilisant typiquement le bruit de Perlin).
De même la couleur du paysage est créée à l'aide du bruit de perlin pour lequel on assigne trois composantes sur chaque canal (R,G,B). De même, on donnera une impression de détail fins sur cette surface en utilisant la technique du multitexturing avec la texture montrée en fig. 38. La couleur sera simplement multipliée par la texture afin de moduler celle-ci.
Fig. 38: [
Texture d'herbe utilisé pour le sol.]Texture d'herbe utilisé pour le sol.
Le terrain est créé de facon à avoir un ravin au milieu afin de permettre le passage de la rivière. Le reste étant déformé par le bruit de perlin. La méthode de construction est la suivante:
//create hole
z = fmin(7*abs((float)(k_y-N_y/2.0)/(float)N_y),1.2);
//add Perlin noise
z += 0.3*noise.get_perlin(x,y,Z0,octave,persistence,frequency);
Le résultat obtenu est affiché en fig. 39.
Fig. 39: [
Sol et rivière.]Affichage du sol et de la rivière en même temps.
On peut finalement encore améliorer la scène en ajoutant une sky box11 afin de donner l'impression d'un paysage à l'horizon. De nombreuses astuces permetterait de rendre la scène encore plus réaliste à moindre frais (ex. voir TP OpenGL et les billboards) mais cela sortirait du cadre de ce projet.
Différentes prises de vues en fig. 40 montrent la scène au complet.
Fig. 40: [
Image de la scène complete avec le bruit de Perlin.]Images de la scène complète avec le bruit de Perlin.
4.4 Bruit de Perlin particulier: Ridged Perlin et son lien avec l'océan
Si le bruit de Perlin permet de modéliser un aspect réaliste de mouvement d'eau rapidement avec un faible nombre d'octaves, on remarque que les crêtes sont d'aspects lisses.
Ainsi, pour une scène mettant en place une rivière ou un lac, ce type de bruit convient tout à fait. Par contre, si l'on souhaite maintenant animer une partie d'océan plus agitée, les vagues doivent posséder des crêtes plus pentues.
On pourrait penser au premier abord que l'augmentation du nombre d'octaves permetterait d'améliorer cet aspect. Cependant, comme nous l'avons vu pour la création du paysage, l'augmentation de ce nombre d'octaves va donner un aspect montagneux à la surface d'eau. Cela n'est évidemment pas souhaitable et le bruit de Perlin simple ne va pas suffire. On va rechercher à accentuer les pentes sans pour autant bruiter plus les creux.
Nous introduisons alors une variante du bruit de Perlin: le Ridged MultiFractal Perlin, ou, dans sa version francais, le bruit multifractale de Perlin à crêtes. Cette variante est connue pour pouvoir produire des montagnes naturelles avec des pics raides, et nous allons l'utiliser ici pour modéliser un océan agité.
Le nom de crête (ridged) est ici évident car l'on souhaite obtenir un bruit plus pentu. On pense évidemment à l'utilisation de la valeur absolue pour réaliser cet effet.
Par contre le terme de multifractale nécessite une explication plus précise. La nature multifractale provient ici de la variation de la dimension fractale [26] (de ses caractéristiques) en fonction de l'altitude. En effet, dans les vallées, le bruit sera atténué, alors que sur les crêtes, la fonction sera plus accidentée.
Cette effet sera en partie créé par l'élévation au carré du bruit (et par la multiplication pondéré des octaves précédentes).
Commençons par considérer le bruit de Perlin γ que l'on centre désormais entre [−1,1].
La création de crêtes se réalise alors par la mise en place de la valeur absolue sur cette fonction |2γ−1|.
Ces crêtes sont maintenant situées en bas de la fonction (proche de zéro). Afin d'obtenir les crêtes situées sur la partie haute de la fonction, on renverse celle-ci en calculant 1−|2γ−1|.
Afin de pouvoir gérer par la suite comment la nature fractale de la fonction va jouer en fonction de l'altitude, on prend en réalité un paramètre L généralement proche de 1 afin de retourner la fonction avec L−|2γ−1|.
Finalement, afin de donner des crêtes plus pentues et de rendre les creux plus doux, on élève le résultat au carré.
On obtient alors la fonction de base du bruit de Perlin à crêtes dénoté par μ avec
|
μ(x)= |
⎛
⎝ |
L−|2γ(x)−1| |
⎞
⎠ |
2
.
|
Fig. 41: [
Étapes de la construction du bruit de Perlin à crêtes.]Étapes de bases de la construction du bruit de Perlin à crêtes μ. La première image montre un bruit de Perlin simple centré en 0. La seconde étape consiste en la prise de la valeur absolue afin de créer les crêtes. Ensuite, l'étape 3 consiste à renverser la fonction précédente afin d'avoir les crêtes en haut. Le renversement est réalisé par l'inversion puis la translation par le paramètre L proche de un. Enfin l'étape suivante est l'élévation au carré afin d'accentuer les crêtes.
On peut ensuite donner la nature fractale à ce bruit. Pour cela, on va sommer, comme pour le bruit classique, des contributions à des échelles et des amplitudes variables.
On va tout d'abord faire décroître l'amplitude suivant le paramètre H en calculant μ(x)+Σk a−k Hμ(ak x). Plus H sera grand, plus les contributions vont avoir une amplitude faible sur l'octave suivante et donc la fonction deviendra uniformément lisse.
Afin de donner l'aspect multifractale, on va pondérer le bruit additionné au cours des octaves par des poids dépendants de l'altitude de l'octave précédente. On limite la contribution de ce poids aux valeurs comprises entre 0 et 1.
On obtient donc la relation μ(x)+Σk a−k Hωk(x) μ(ak x), avec ω le poids donné suivant l'altitude précédente et donné par la relation ωk(x)=max(min(ωk−1(x) α μ(ak x),1),0), avec α permettant de gérer l'importance du bruit précédent. C'est de ce paramètre dont va dépendre la nature multifractale du bruit.
Au final, le bruit de Perlin à crêtes peut donc s'écrire par la relation
|
|
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩ |
| μp(x) = μ(x |
)+ |
|
ωk(x) a−k H μ(ak x) |
|
| |
⎧
⎨
⎩ |
| ωk(x)=min(max(α ωk−1(x) μ(ak−1x),0),1) |
| ω0(x)=1; |
|
|
|
|
|
(19) |
Fig. 42: [
Sommation d'octaves du bruit de Perlin à crêtes.]Exemple de sommation d'octaves dans le cas du bruit de Perlin à crêtes. La figure de gauche montre la sommation de deux octaves alors que la suivante montre la sommation de trois.
Par la suite, la fig. 43 montre l'effet des différents paramètres de ce bruit.
Fig. 43: [
Effet des parametres du bruit de Perlin à crête.]Effet des paramètres pour le bruit de Perlin à crêtes. La première image montre le bruit lorsque le paramètre a est pris grand (ici 6), les fréquences sommées sont alors plus hautes dès les premières octaves, on passe donc rapidement de grands pics à des pics faibles mais de fréquences importantes. Les figures 2 et 3 montrent l'effet de l'offset sur l'apparence de la courbe. Pour un offset L important (figure 2, L=1.4), les hauteurs sont plus importantes, il y a donc peu de différence entre les crêtes et les creux qui sont également accidentés. Au contraire pour la figure trois où L=0.9, seul les crêtes sont bruitées alors que les creux restent très lisses. Enfin le paramètre H est modifié dans les figures 4 et 5. En effet, pour la figure cinq, on prend H important (H=1.2) ce qui donne une diminution très importante des contributions dès les premières octaves, le bruit apparaît donc peu accidenté. Au contraire, sur la dernière figure, on choisit H=0.2, la décroissance en amplitude des contributions de grandes amplitudes est alors plus réduite, on obtient donc plus de bruit. On peut bien remarquer sur cette image que les crêtes hautes sont plus bruitées que les creux.
Un exemple 2D est finalement réalisé avec Matlab est montré en fig. 44.
Fig. 44: [
Bruit de Perlin à crêtes en 2D.]Bruit de Perlin à crêtes réalisé en 2D avec Matlab. Les filaments partants des crêtes et un fond peu bruité est caractéristique de ce bruit.
4.4.2 Implémentation en OpenGL et limitations
On va maintenant implémenter ce bruit sous OpenGL. La mise en place du bruit de Perlin à crêtes n'est pas particulièrement compliqué à coder une fois que l'on dispose du bruit de Perlin de base.
Le code complet de la fonction est le suivant
float Perlin_noise::get_ridged_multifractal_perlin(float x,float y,float z,
float H,int octave,float frequency,float offset,float threshold)
{
int k_octave=0;
float signal=0.0;
float result=0.0;
float weight=0.0;
//calculate first pass
signal = get_perlin(x,y,z);
signal = offset-fabs(signal);
signal *= signal;
result = signal;
weight = 1.0;
//sum octaves
for(k_octave=0;k_octave<octave-1;k_octave++)
{
rand_octave = (int)((k_octave<<13)*4321+234);
x *= frequency;
y *= frequency;
z *= frequency;
weight = signal*threshold;
//truncate weight
if(weight>1)
weight=1;
else
if(weight<0)
weight=0;
signal = get_perlin(x,y,z);
signal = offset-fabs(signal);
signal *= signal*weight;
//sum contributions
result += signal*powf(frequency,-(float)k_octave*H);
}
return result;
}
Afin d'utiliser le bruit de Perlin à crêtes, on se place maintenant dans le cas d'une plage afin de voire la mer dont les vagues sont plus agitées que dans le cas d'une rivière.
La plage modélisée consiste simplement en un terrain en pente avec une étendue d'eau se prolongeant d'un seul coté. Le terrain est construit comme précédemment à l'aide d'un bruit de Perlin. Lors de l'ajout de l'eau et d'une unique onde sinusoïdale sur la hauteur des vertex, on obtient la vue montrée en fig. 45
Fig. 45: [
Plage et mer modélisée par un unique sinus.]Aspect de la plage choisie et de la mer modélisée pour l'instant par un unique sinus sur l'axe z.
On ajoute ensuite un simple bruit de Perlin d'amplitude faible afin de simuler les remous pouvant avoir lieux, notamment à l'approche de la plage. Le résultat est montré en fig. 46.
Fig. 46: [
Mer avec sinus plus bruit de Perlin simple.]Les vagues de la mer sur la plage avec ajout du bruit de Perlin simple afin de donner un effet plus naturel qu'un simple sinus. On remarquera que pour améliorer le réalisme, on rend la mer plus transparente sur la côte qu'au large où la hauteur de l'eau est sensée la rendre plus opaque.
Cependant, on remarque bien ici que la mer possède toujours de petites vagues lisses. On va maintenant ajouter le bruit de Perlin à crêtes afin de donner l'impression de vagues plus pentues. On notera que ces vagues ne doivent pas avoir lieu sur la plage elle même mais plus au loin dans la mer, ainsi on fait dépendre l'amplitude de ces vagues en fonction de l'éloigment par rapport à la plage.
La fonction utilisée pour le déplacement en hauteur des vertex de la mer est donnée par:
//sinus
z = 0.03*cos(4*y-ct/2);
//Perlin
z+= 0.04*noise.get_perlin(x,y,Z0+ct/10,octave,persistence,frequency);
//Ridged Perlin
z+= 0.1*noise.get_ridged_multifractal_perlin(x/2,y/2-ct/5.0,z/2-ct/10.0,
0.7,4,2,1.1,0.8)
*
(N_y-k_y)/(float)N_y;//depends on the distance to the beach
Et le résultat est affiché en fig. 47. Différentes prises de vue de la scène sont également prises et affichées en fig. 48.
Fig. 47: [
Résultats complet de la mer avec le bruit de Perlin à crête.]Résultats obtenus avec le bruit de Perlin à crêtes. Le premier plan de la plage est consitué d'eau transparente avec la contribution principale du sinus et du bruit de Perlin simple. L'arrière plan de la mer plus profonde et moins transparente est consituée du bruit de Perlin à crêtes provoquant des vagues beaucoup plus pentues.
Fig. 48: [
Prises de vues de la mer avec le bruit de Perlin à crête.]Différentes prises de vues de la mer réalisées à l'aide du bruit de Perlin à crêtes. La première image montre l'aspect général de la plage avec l'eau transparente et peu agitée sur la côte, et les vagues plus importante au large. La seconde image montre le terrain avec la mer au fond. La troisième image montre l'aspect de la mer et de la plage vue de haut. La quatrième image montre la mer se jettant sur la plage vu de derrière. La cinquième et la sixième images sont des vues de derrière au niveau de la mer, à la hauteur des vagues importantes. La septième image montre la grille utilisée sur les vagues. L'avant dernière image montre la construction du terrain en dégradé et enfin la dernière image est une vue d'ensemble de l'agencement de la scène au milieu de la sky-box.
Les figures à l'arrêts peuvent parraître convaincantes, cependant, on va s'apercevoir d'un problème lors de l'animation. En effet, les fréquences du bruit de Perlin à crêtes sont très élevées et d'amplitudes importantes car ce bruit à été conçu pour. Cependant la grille utilisée dans l'implémentation est uniforme et peu détaillée par rapport aux fréquences des vagues. Ainsi lorsque l'on se trouve en face d'un pic d'une vague, nous ne sommes plus du tout dans les conditions de Shannon comme le montre la fig. 49.
Fig. 49: [
Problème due à l'échantillonnage du bruit haute fréquence.]Problème due à l'échantillonnage grossier du bruit sur les hautes fréquences.
On va alors se rendre compte lors de l'animation que suivant la position de l'échantillonnage d'une image à l'autre, les vagues vont changer d'aspect et osciller en hauteur.
Ainsi la modélisation de vagues à crêtes pose des problèmes de visualisation plus important que les simples vaguelettes créées par le bruit de Perlin simple.
On pourrait prendre une grille plus fine de façon uniforme, cependant on perdrait alors beaucoup en temps de calcul alors que dans les conditions actuelles, le nombre de vertex à calculer à chaque frame est déjà limitant.
Une autre solution plus performante mais plus difficile à mettre en oeuvre serait la ramification de la mesh de façon locale en fonction de la fréquence de la vague. Ainsi les vaguelettes de la côte ne nécessiterait qu'une grille lâche, alors que celle des vagues importantes serait plus fine.
Afin d'utiliser pleinement ce bruit et de ne plus être limité par la grille, nous avons choisi de contourner le problème tout en ouvrant une nouvelle voie de visualisation. Pour cela nous avons fait le choix de réaliser le rendu de ces vagues par la méthode de ray-tracing. Cette méthode permet en effet d'échapper à tout problème de taille de la grille car cette fois les vertex seront de la taille des pixels.
4.5 En Résumé
-
Le bruit multifractale de Perlin à crêtes est une variante du bruit de Perlin.
- Il est construit à l'aide de la prise de valeurs absolues, d'une translation et inversion puis d'une élévation au carré.
- Il permet de modéliser des pics plus abruptes et donc des vagues raides de l'océan.
- Les pics les plus hauts sont les plus accidentés (aspect multifractal)
- Nécessite un échantillonnage fin pour profiter des hautes fréquences.
5 Visualisation par Ray Tracing
You know you have been raytracing too long when ...
... You want to cheat and look at nature's source code.
— Mark Stock
5.1 Introduction
5.1.1 Généralitées
3NOUS
allons maintenant réaliser les visualisations par la méthode de Ray-Tracing en utilisant le logiciel open source Pov-Ray (Persitence Of Vision Ray Tracer).
Nous rapellons très brièvement que la méthode de visualisation par ray-tracing correspond à envoyer pour chaque pixels de l'image finale un rayon identifiable à un rayon lumineux. Celui ci va parcourir la scène 3D jusqu'à intersecter un objet, à partir de la, le rayon va se diriger vers la/les source(s) de lumière(s) afin de calculer la couleur correspondante au pixel.
Les objets peuvent donc être définis de façon mathématique (et non plus seulement par des triangles/quads) car seule l'intersection entre l'objet et la ligne droite du rayon va entrer en compte.
Les avantages du Ray-Tracing sont les suivants:
-
Aucun problème d'échantillonnage par vertex car les objets sont mathématiques (ex. une sphère correspond à une vraie sphère et non un assemblage de triangles) et l'échantillonnage est réalisé au niveau de la taille du pixel de l'image.
- Certains effets physiques sont simples à mettre en oeuvres. Les ombres notamment sont automatiquement gérées par la méthode, mais on peut également penser à la transparence, la réflexion et la réfraction utile au niveau de la visualisation des fluides.
- Grande finesse des images pouvant avoir un aspect photoréaliste (encore difficile à réaliser par les cartes graphiques actuelles).
Quelques exemples d'effets directement réalisable ou simulés par ray-tracing sont montrés12 en fig. 50.
Fig. 50: [
Exemples d'effets physiques réalisable en ray-tracing.]Figures montrant certains effets physiques réalisables avec la technique du ray-tracing. La permière figure est un exemple de l'utilisation de la reflection sur des objets simples. La seconde figure montre l'utilisation de la transparence combinée à la réfraction donnant l'aspect de verre (utile pour modéliser l'eau). Enfin la dernière image montre une technique permettant de simuler la dispersion des longueurs d'ondes sur un prisme (effet complexe qui n'est que simulé).
Par contre le ray tracing souffre d'un inconvénient majeur résidant dans le principe même de la méthode; à savoir que le rendu est très lent. Nous sommes ici très loin du temps réel car le rendu d'une seule image d'une scène un peu complexe peu dépasser très largement l'heure de calcul.
Si les scènes graphiques actuelles sont de plus en plus rapidement calculées par les cartes graphiques, celles-ci ne sont malheureusement d'aucune utilité pour les méthodes classiques de ray-tracing. En effet, le ray-tracing consiste à calculer de très nombreuses équations d'intersections pour chaque pixel du rendu. La méthode fait donc appel quasi exclusivement au CPU.
Afin d'obtenir un rendu plus “rapide”, les innovations viennent donc des processeurs centraux. Ainsi la méthode va bénéficier notamment des nouvelles technologies des processeurs quatres coeurs. En effet il est assez aisé de réaliser un rendu de ray-tracing en parallèle (chaque processeur pouvant réaliser le calcul de pixels différents de l'image de façon indépendante).
Dans le cadre de ce rapport, les images ont été calculées sur un processeur simple de portable mono-thread datant de quatre ans ce qui ne permet pas de réaliser le rendu de scènes très complexes en un temps raisonnable.
On pourra finalement tout de même évoquer que les cartes graphiques modernes programmables permettent cependant d'émuler des calculs de type ray-tracing. La vitesse de calcul est donc décuplée et une approche temps réel est possible. Cependant certaines limitations restent inhérente à l'émulation (on est contraint de décrire la scène sous forme de triangles, ...). Une présentation intéressante des effets nécessaire au rendu réaliste de fluide appliqué en temps réel sur carte graphique en simulant les équations du ray-tracing est donné en [28].
5.1.2 But de la partie
Le but de notre approche est donc de donner un rendu beaucoup plus réaliste à l'eau grâce aux effets physiques tels que la réflexion et la réfraction.
On souhaitera donc utiliser cette méthode afin de pouvoir exploiter correctement le bruit de Perlin à crêtes notamment sans avoir à ce soucier de l'échantillonnage.
Enfin on réalisera des animations totalement précalculées en réalisant le rendu d'un grand nombre d'images puis en les rassemblants à la fin.
5.1.3 Introduction à Pov-Ray
Pov-Ray est un logiciel open source assez connu dans le cas du ray-tracing. Il est développé par une équipe dynamique et des mises à jours sont réalisées fréquemment. (intégration des architectures 64 bits13, ...).
La qualité de ses rendus sont tout à fait à la hauteur des logiciels professionnels commerciaux et possèdent des effets avancés (photon mapping, radiosité, ...).
Nous remercions Gilles Tran, Christoph Hormann et Ben Weston pour les exemples fournit dont nous nous sommes inspirés.
La description de la scène se réalise sous forme de scripts en mode texte ce qui rend sont utilisation peu conviviale de prime abord. Cependant, elle permet ainsi une grande souplesse d'utilisation et d'interaction avec des logiciels exterieurs simplement par chargement de fichiers textes14.
La scène se composera comme habituellement par une caméra, la présence d'au moins une lumière puis la description des objets.
Des objets de bases sont disponibles et notamment toute surface définie par une isosurface peu être rendu directement.
Chaque objet possède ensuite des attributs de positions et de tailles mais également d'interaction avec le rayon permettant de lui donner sa couleur (couleur du matériaux, transparence, reflexion, perturbation de la normale, ...).
Enfin un certain nombre de fonctions mathématiques sont disponibles directement dans le logiciel. Beaucoup d'entre elles sont utilisées en tant que modification de la couleur ou des normales de l'objets. On notera notamment la présence du bruit de Perlin simple et de sa variante à crêtes.
On donne ici la structure de base d'un fichier de description de scène classique au format Pov-Ray dessinant une sphère rouge:
//define a camera
camera
{
location <-5,5,0>
look_at <0,0,0>
}
//define a light
light_source
{
<-1,8.5,-6> //position
color rgb <1,1,1>//color
}
//define an object sphere
sphere
{
<0,0,0> //position
1 //radius
pigment
{
color rgb <1,0,0> //color
}
}
5.2 Mise en place de la scène de Base
Nous allons réaliser les figures sur une même scène de base. Pour cela, nous mettons tout d'abord en place une surface plane d'équation z=0 comme le montre la fig. 51. Cette surface est définie comme réfléchissante ce qui permettera de donner l'impression de liquide.
#declare water=
plane
{
y,0
pigment{color rgb <0.3,0.3,0.7>}
finish{reflection{0.1,1.0 fresnel}}
}
Il est alors important d'avoir un sol en dessous de la surface afin de pouvoir rendre celle-ci transparente (si il n'y a pas de sol, la surface ne va pas se distinguer du ciel). Nous ajoutons donc un sol gris. Celui-ci est réalisé par l'ajout d'un sphère et non d'un simple plan afin de ne pas le créer jusqu'à l'infini lorsque l'on réalisera le rendu d'une surface liquide non infinie15.
La texture d'eau transparente et ces attributs au complet sont détaillés ici
plane
{
y,0
texture
{
pigment{color rgbt <1,1,1,1>} //color transparent
finish{reflection{0.1,1.0 fresnel}}//reflection
}
interior//refraction and attenuation through the surface
{
ior 1.33 //refraction ior=index of refraction
media //absorbtion
{
absorption rgb <2,2,1>
density{rgb 0.1}
}
}
}
Ensuite, il convient d'avoir un ciel correct afin d'obtenir la reflection de celui-ci sur l'eau ce qui améliore grandement le réalisme. Pour cela, on utilise la technique des nuages expliquée dans la partie précédente du rapport (voir chap. 4.2.4).
Les nuages sont disposés sur une sphère et on utilise le bruit de Perlin disponible sous la forme de la fonction f noise3d de Pov-Ray
#declare perlin = function{f_noise3d(x,y,z)}
#declare fn_sum = function(x,y,z){perlin(5*x,5*y,5*z)+0.2*perlin(14*x,14*y,14*z)}
sky_sphere //special sky sphere avoid problem of scaling
{
//clouds
pigment
{
function{1-min(1.6*fn_sum(x,y,z),1)}
colour_map
{
[0.0 color rgb <0.7,0.7,1>]
[0.6 color rgb <1,1,1>]
}
}
//white horizon
pigment
{
gradient y
color_map
{
[0.0 color rgbt <1,1,1,0>]
[0.15 color rgbt <1,1,1,1>]
[0.85 color rgbt <1,1,1,1>]
[1.0 color rgbt <1,1,1,0>]
}
}
}
On remarquera également que l'on rajoute une coloration suivant l'axe verticale permettant de rendre l'horizon uniformément blanc tel que cela se produit dans les scène naturelles.
Finalement, on ajoute un petit cylindre simple sur la surface pour visualiser l'effet de la réflection sur un object.
Les différentes étapes de la construction de cette scène de base sont résumés en image en fig. 51.
Fig. 51: [
Construction de la scène de base sous Pov-Ray]Étapes de la construction de la scène de base sous Pov-Ray. La première étape consiste à créer une surface plane réflechissante d'altitude nulle. Ensuite, on ajoute un sol et on rend la surface transparente. Finalement, on ajoute le ciel réalisé par un bruit de Perlin puis un cylindre au milieu de la scène afin de voir l'interaction de sa reflection avec la surface liquide.
5.3 Cas du Bump Mapping
Le bump mapping correspond à une méthode très simple permettant de donner l'impression de relief sur une surface ne l'étant pas vraiment.
Pour cela, on considère par exemple un plan horizontal dont les normales sont donc toutes supposées verticales.
Pour donner l'impression d'un relief, on va perturber l'orientation des normales de la surface, ainsi l'effet diffus et spéculaire de la lumière est modifié et va donner des régions plus sombres ou plus claires suivant l'orientation de cette normale.
Cet effet va permettre de simuler une orientation tridimentionnelle de la surface alors que celle-ci est en réalité plane.
Cet effet peut se réaliser en OpenGL, mais il faut pour cela, soit un nombre important de normales et donc de vertex pour obtenir un relief fin, soit jouer directement au niveau de la texture. Un exemple de texture d'eau associé à du bump mapping implémenté sous OpenGL dans le cadre d'un TP est montré en fig. 52.
Fig. 52: [
Exemple de Bump mapping sous OpenGL]Exemple d'une texture d'eau associé à du bump mapping sur une grille lâche sous OpenGL.
La méthode du ray-tracing permet également de mettre en place très facilement cet effet sans se soucier du niveau de détail car la normale est définie en chaque pixel.
Nous pouvons donc modéliser cet effet artificiel de vagues en ajoutant une fonction de perturbation de normale dans la description du plan de la surface liquide. Pour cela, on rajoute dans la texture l'attribut
normal{function{f_normal_perturb(x,y,z)}}
avec par exemple f normal pertub défini par un bruit de perlin
#declare f_normal_perturb=function{f_noise3d(x,y,z)}
Le résultat est alors affiché en fig. 53.
Fig. 53: [
Bump mapping appliqué sur une surface avec un bruit de Perlin.]Bump mapping appliqué sur la surface liquide plane avec un simple bruit de Perlin.
On remarque que l'aspect du liquide à l'horizon est très bien rendu. Le bump mapping permet donc de donner l'impression d'eau sur une grande étendue à moindre frais. Au premier plan, la surface peut parraître déformée, cependant, une visualisation attentive permet de se rendre compte que la surface reste plane. La réflection du cylindre est bien rendue et permet d'accroître le réalisme, par contre l'ombre de celui ci trahit la mise en place de l'astuce. En effet cette ombre est totalement plane et n'est évidemment pas déformée par l'action sur les normales.
On peut évidemment mettre en place le bruit de Perlin à crêtes afin de donner des impressions de relief beaucoup plus pentues. Le résultat est montré en fig. 54.
Fig. 54: [
Bump mapping à l'aide du bruit de Perlin à crête.]Bump mapping réalisé à l'aide du bruit de Perlin à crêtes.
La méthode du bump mapping permet donc des résultats assez convainquants pour un coup faible au niveau du temps de calcul car on peut le réaliser sur une surface plane.
Cependant, si l'effet permet de simuler l'horizon de l'océan de facon très réaliste, on est limité par le fait que la surface reste plane. Pour cela, la déformation de celle-ci est un passage nécessaire pour obtenir une qualité donnant une impression de réalisme.
5.4 Height Field
Nous allons maintenant réaliser la déformation par l'utilisation de la méthode de heigh field.
La méthode est semblable à celle que l'on a utilisée sous OpenGL dans la deuxième partie pour présenter le bruit de Perlin. En effet, pour chaque position (x,y) définie comme fixe sur un plan, on évalue un z donné afin de le transcrire en altitude.
L'utilisation en ray-tracing de cette méthode nous fait donc perdre l'avantage de ne plus avoir à considerer de vertex puisque ceux-ci définissent la surface. De même la surface ne peut plus être de dimension infinie.
D'un autre coté, le fait de ne plus définir la surface de façon continue permet le précalcule des vertex et ainsi un affichage relativement rapide (comparé aux méthodes d'isosurfaces que nous verrons par la suite). Par contre, si l'on souhaite une qualité suffisante, la place mémoire prise par le précalcule des vertex n'est pas négligeable.
On définit alors une fonction de type bruit de Perlin définissant la hauteur de la surface. Dans le cas d'un bruit de Perlin simple, on peut définir la hauteur par
#declare f_perturb=function{f_noise3d(x,y,z)
+ 0.5*f_noise3d(2*x,2*y,2*z)
+ 0.25*f_noise3d(4*x,4*y,4*z)
+ 0.125*f_noise3d(8*x,8*y,8*z)}
Puis on l'applique à un objet de type height field avec un nombre suffisant de vertex. On obtient alors le rendu obtenu en fig. 55.
On peut également réaliser le rendu avec un bruit de Perlin à crêtes. Cette fois, on utilise la fonction:
#declare f_perturb_ridged=function{f_ridged_mf(x,y,z,0.5,2,7,1.0,0.8,0)*0.5}
Le résultat est également affiché en fig. 55.
Fig. 55: [
Rendu de height field avec bruit de Perlin par ray tracing.]Rendu de height field par ray-tracing avec le bruit de Perlin (première image) et le Bruit de Perlin à crêtes (seconde image).
On peut voir que le bruit de Perlin simple permet effectivement de modéliser correctement une impression de lac ou de ruisseau. Au contraire, le bruit de Perlin à crête de la seconde image est ici correctement rendu du au grand nombre de vertex et permet de donner une impression de vagues sur la mer.
On pourra notamment comparer la première image à une image témoin réelle d'eau prise sur un lac tiré de l'article de Thon et al. [29] que l'on montre en fig. 56.
Fig. 56: [
Comparaison avec une photo d'eau réelle.]Image réelle d'eau prise sur un lac. Image provenant de [29].
La méthode permet donc d'obtenir une bonne qualité de visualisation tout en préservant une relative rapidité d'affichage pour du ray-tracing16 dans la mesure où l'on dispose de suffisement de mémoire.
Une autre méthode est encore plus puissante et possède d'autres avantages, il s'agit de celle du rendu par isosurface.
5.5 Isosurface
Le rendu d'isosurface à déja été introduit dans la seconde partie du rapport au chap. 2.
La fonction implicite est ici totalement définie de façon mathématique. Ainsi il n'y a pas de précalcules, donc la mémoire RAM n'est pas utilisée. Par contre il faut rechercher l'intersection de la surface pour chaque rayon envoyé. Le calcul est donc typiquement très long dès que la fonction implicite possède un gradient important.
On rapel également que le rendu d'isosurface est intéressant de par l'indépendance de la surface à sa topologie. Ainsi, lors de l'utilisation des height fields, la surface était toujours contrainte à pouvoir être définie par z=f(x,y) comme la déformation d'un plan. L'isosurface permet d'écarter totalement ce problème et est capable de modéliser des fonctions multivaluées (comme les vagues en rouleaux) ou des petites gouttes non connexes au dessus des vagues.
De plus, les isosurfaces peuvent être combinées simplement à l'aide d'opérateurs tels que min et max et de façon continue17, on peut alors imaginer combiner la surface fluide à une autre isosurface représentant une rivière ou une cascade par exemple.
L'utilisation de cette méthode possède également l'avantage qu'il est facile de définir un dedans et un dehors à l'isosurface (dedans étant par exemple défini par ϕ(x)<0 et dehors par ϕ(x)>0 avec les notations du chap. 2. On peut ainsi gérer la refraction également avec cette méthode.
Pov-Ray permet de gérer directement le rendu d'isosurface bien que celui-ci soit plus long.
On utilise ici la méthode présentée précédamment en prenant initialement une fonction implicite donnée par ϕ(x,y,z)=z et la recherche des racines ϕ(x,y,z)=0 donne évidemment le plan horizontal passant par l'origine.
On va alors déformer ce plan en utilisant le bruit de Perlin.
5.5.2 Cas d'un petit rectangle
On va maintenant créer l'isosurface sur une petit portion de l'écran et couper les bords par des plans. Pour cela, on défini l'isosurface par
isosurface
{
//function
function { y-0.6-f_perturb(x/2, y/2, z/2)/2.5 }
//container
contained_by { box { <-2,0.0,-2>, <2,1.5,2> } }
//texture
texture
{...
}
en utilisant la même texture que pour les cas précédants.
On utilise initialement le bruit de Perlin simple en déclarant ϕ(x,y,z)=y−γp(x,y,z) avec trois octaves, on obtient alors le résultat montré en fig. 57.
Fig. 57: [
Visualisation de l'isosurface coupée pour un bruit de Perlin simple.]Visualisation de l'isosurface pour une petite portion coupée avec un bruit de Perlin simple.
L'indice de réfraction de la surface liquide est pris de 1.33 ce qui est censé modeler l'indice de réfraction de l'eau. On remarquera l'ombre du poteau sur le sol se reflétant sur le mur opposé tel que l'on pourrait le voir dans un aquarium par exemple.
L'allure de l'eau est globalement la même que celle que l'on pouvait obtenir avec la height field car le liquide est relativement calme.
On peut également utiliser le bruit de Perlin à crêtes. Cette fois les vagues vont être plus agitées. En utilisant uniquement ce bruit, on peut obtenir alors l'image montrée en fig. 58.
Fig. 58: [
Visualisation de l'isosurface coupée pour un bruit de Perlin à crêtes.]Visualisation de l'isosurface pour une petite portion coupée avec un bruit de Perlin à crêtes.
On peut remarquer que l'effet de l'eau est réellement bien rendu et donne l'impression de vagues agitées.
L'effet de surface agitée apparaît ici mieux rendu (plus agité avec des formes moins classiques) que pour l'utilisation de la height field simple. En effet, pour le cas où l'on ne décrit que la hauteur z en fonction de (x,y), on a un bruit toujours continu d'aspect montagneux, ainsi les vagues que l'on pouvaient voir en fig. 55 pour le cas du bruit de Perlin à crêtes variaient toujours de façon continu avec x et y. Dans le cas de l'isosurface, non seulement z est modulé par le bruit mais également x et y. La vague peut alors prendre une forme qui n'est plus contrainte à rester du type “colline”.
Au delà, si l'on continue à rendre la surface encore plus bruitée, on va pouvoir obtenir des fonctions qu'il n'est plus possible de modéliser sous la forme z=f(x,y) de part leur nature multi-valuées ou par l'apparition de trous.
Un exemple est ainsi montré en fig. 59 où l'on a augmenté le paramètre α de l'équation 19 du chap. 4.4.1 correspondant au facteur multiplicatif de la contribution des octaves précédants (on augmente le bruit sur les crêtes).
Fig. 59: [
Visualisation de l'isosurface coupée pour un bruit de Perlin à crêtes avec un gain important.]Visualisation de l'isosurface pour une petite portion coupée avec un bruit de Perlin à crêtes dont le bruit est plus important en ayant augmenté le paramètre α. Ce type de surface n'est plus décrivable par une fonction du type z=f(x,y). L'utilisation d'une isosurface18 prend ici tout sont sens.
On peut alors observer quelques détails de cette dernière image montrant la complexité de la surface. Un zoom est ainsi réalisé en fig. 60.
Fig. 60: [
Zoom sur une portion de l'isosurface.]Zoom sur une portion de l'isosurface déformée par le bruit de Perlin à crêtes. Les figures sont prises sur la partie gauche du rectangle de liquide. La première image est créée en prenant un bruit sur 3 octaves. On peut y distinguer une vaguelette ne pouvant pas ce définir par une fonction de type height-field qui correspondrait à cet endroit à plusieurs valeurs de z pour la même abscisse. L'aspect donné par le zoom sur la surface donne une impression de glace car les coupures sont très droites. Pour améliorer un peu cette effet, la seconde image est réalisée en augmentant le paramètre H et en prenant cette fois 4 octaves (on prend des fréquences plus élevées, mais leur contribution décroit plus rapidement). On obtient alors des vagues beaucoup plus accidentées donnant moins l'impression de glace. On remarquera, à la droite de la vaguelette, une goutte quasiment détachée du reste du liquide.
5.6 Visualisation de surfaces étendues
On peut également profiter du rendu par isosurface pour le cas de surface étendue. Il suffit pour cela de réaliser le rendu pour une surface plus importante. Le temps de calcul devient alors très long, une image de 1280× 960 pouvant alors demander (avec l'antialiasing) plus de trois heures de calcul sur le PC dont nous disposons.
Nous montrons également ici un exemple pour le cas du bruit de Perlin simple et pour le cas du bruit de Perlin à crêtes. Un exemple est ainsi montré en fig. 61.
Fig. 61: [
Rendu de surface étendues par isosurface.]Rendu de surface liquide étendue de type lac ou océan par la méthode des isosurfaces en ray-tracing. La première image est réalisée entièrement avec un bruit de Perlin simple, la seconde est réalisée avec un bruit de Perlin à crêtes.
Le cas du bruit du Perlin à crêtes peut être modifié afin de rendre l'image un peu plus réaliste, en effet on remarque que l'océan est d'un bleu trop uniforme.
Dans ce cas, il est possible de rajouter, comme dans le programme OpenGL, une coloration dépendante de l'altitude z.
Pour cela, on rajoute un gradient de couleur allant du bleu au blanc en fonction de la position sur la vague.
Ensuite, pour améliorer le réalisme, on en peut encore donner un effet de perturbation sur le haut des vagues. Cela revient en fait à accentuer l'effet multifractale du bruit. On peut notamment penser à de la mousse qui se forme lors des remous de l'agitation des vagues.
On peut alors soit implémenter cette perturbation directement sur le bruit, où bien, comme celui-ci doit être d'amplitude faible, on peut le réaliser à moindre frais en utilisant du bump mapping. Pour cela, on implémente une déformation de bump mapping donnée par une fonction de bruit de Perlin qui va déformer de plus en plus les normales suivant l'altitude de la vague.
L'ensemble de la texture est implémenté par le script Pov-Ray suivant.
texture
{
pigment_pattern
{
//varie suivant la hauteur
gradient y
}
texture_map
{
[0.0 //bas de vague
pigment{color rgbt <1,1,1,1>}
finish{reflection{0.0,1.0 fresnel}}
]
[0.25
pigment{color rgbt <1,1,1,1>}
finish{reflection{0.0,1.0 fresnel}}
]
[0.33 //haut de vague
pigment{color rgbt <1,1,1,0.3>}
finish{reflection{0.2,1.0 fresnel}}
normal
{
bozo 1.0 //correspond au bruit de Perlin simple
translate <0,-0.5,0>
scale <1,2,1>*0.003
}
]
}
Le résultat est alors affiché en fig. 62. On notera que la mise en place de textures dépendantes de paramètres ralentit encore plus le rendu. Cette simple image a en effet mis 6 heures à être rendu.
Fig. 62: [
Surface étendue avec changement de couleur et bump mapping.]Rendu de surface étendue par isosurface avec un bruit de Perlin à crêtes. La couleur et le bump mapping varient en fonction de l'altitude de la vague.
Enfin, on pourrait également simplement augmenter le gain du bruit α (contribution des octaves précédentes) sur la même image. Cela permet d'avoir des vagues beaucoup plus accidentées donnant l'impression de la présence d'un vent important au dessus de l'eau.
On rajoute dans notre cas uniquement 0.3 au gain du bruit.
#declare f_normal_perturb_ridged=
function{f_ridged_mf(x+abs(y)/1.2,y,z,0.86,2.5,7,1.0,0.8+0.3,0)}
On observe alors dans ce cas le résultat de la figure 63.
Fig. 63: [
Surface étendue avec un gain important.]Rendu de surface étendue par isosurface avec un bruit de Perlin à crêtes. La gain est cette fois plus important d'où la présence de vagues plus accidentées.
5.7 Interpolation entre les bruits
Dans le cadre de modélisation de plages ou de cascades par exemple, il peut être intéressant de réaliser des transitions entre des vagues agitées et des vagues plus calmes. Il parrait assez évident de choisir un bruit de Perlin à crêtes pour les vagues agitées et un bruit de Perlin simple pour les régions plus calmes.
Nous testons alors le cas de la transition le long d'une bande de liquide. Les surfaces agitées et calmes sont montrées en fig. 64
Fig. 64: [
Bandes de liquide de base.]Visualisation des bandes de fluides utilisées. La première bande est réalisée par un bruit de Perlin simple alors que la seconde est donnée par un bruit de Perlin à crête.
Les deux bandes ainsi présentées peuvent servir de fonction de base pour en réaliser différentes combinaisons. On rapelle les notations de γ et μ pour la désignation respective des bruits de Perlin simple et à crêtes.
L'interpolation linéaire entre ces deux bruits du type est donnée par
f(u)=u γ + (1−u) μ
,
où u représente une variable normalisée variant entre 0 et 1 d'un bout à l'autre de la bande de test.
Cette simple interpolation permet alors d'obtenir le résulat montré en fig. 65.
Fig. 65: [
Interpolation sur les deux bruits le long de la bande.]Interpolation entre le bruit de Perlin à crête à gauche et le bruit de Perlin simple à droite le long de la bande de liquide.
On peut alors bien visualiser le passage lisse d'une fonction à l'autre permettant de donner deux types d'agitation de l'eau bien distincts.
L'exemple de la définition de l'isosurface en code Pov-Ray est alors du type
isosurface {
function {
y-0.3
-
gamma(x/4.0, y/4.0, z/4.0)/1.3 * (z+4)/8
-
mu(x/1.5,y/1.5,z/1.4)/3 * (1-(z+4)/8)
Enfin, un autre type de forme peut être réalisé par une autre fonction d'interpolation. Cette fois, cette interpolation se réalise uniquement par le passage du bruit de Perlin à crêtes à son opposé. On a alors f(u)=u μ+(1−u) (−μ), soit
f(u)=(2 u−1) μ
.
La partie négative du bruit de Perlin à crête va donc se soustraire au niveau de la surface définie implicitement ce qui créé des impressions de remous.
Le résultat de ce type de fonction est ainsi montré en fig. 66
Fig. 66: [
Interpolation du bruit de Perlin à crêtes le long de la bande.]Interpolation entre le bruit de Perlin à crête (gauche) et son inverse (droite) de long de la bande de liquide.
L'impression permetterait notamment de modéliser correctement l'approche d'une plage où les remous se situeraient du coté peu profond.
5.8 Cas de scènes complexes
Maintenant que nous disposons d'une surface d'eau pour laquel nous controlons les différents paramètres, il est relativement aisé d'inclure cette surface dans des scènes pouvant comporter plus d'éléments.
Un exemple de scène est ainsi proposé. Pour cela, nous créons une surface de liquide par la méthode de l'isosurface et la déformons par un bruit de Perlin simple comme cela a été présenté auparavant.
Ensuite, un terrain est ajouté à la scène. Ce terrain est réalisé simplement par une height field. Et la déformation de celui-ci est donné également par un bruit de Perlin comme présenté dans le cas d'OpenGL au chap. 4.3.3. La couleur du terrain est également modulé selon un bruit de Perlin.
Le résultat proposé tentant de modéliser un lac est alors montré en fig. 67
Fig. 67: [
Exemple de scène complexe.]Exemple de scène plus complexe mêlant eau et paysage. La première figure montre la scène alors que celle de droite correspond à une vue éloigné montrant sa constitution.
La transparence de l'eau assez peu profonde ici rend la couleur de l'eau légèrement verdâtre car le fond l'est aussi.
La scène reste cependant assez simple, et nous laissons ici le soin aux artistes de réaliser des scènes beaucoup plus complexes.
Enfin, une présentation sur les surfaces liquide ne serait pas complète sans son incontournable scène de coucher de soleil. Nous proposons donc la notre, basée sur cette scène pour laquel l'illumination est placée à la limite de la hauteur de la colline et où la coloration est choisie dans les tons jaunâtres. Le coucher de soleil est alors montré en fig. 68. Un léger brouillard de type dispersif permet de mettre en valeur les rayons du soleil, et par la même occasion, de rendre le rendu excessivement lent.
Fig. 68: [
Exemple de coucher de soleil.]Exmple de coucher de soleil au dessus du lac.
5.9 En Résumé
-
Le Ray-Tracing est une méthode permettant d'obtenir une grande qualité de rendu bien que très lent et inapplicable pour du temps réel.
- Le rendu par height fields est relativement rapide mais est limité par une description de la surface du type z=f(x,y).
- Le rendu d'isosurface est une méthode très puissante permettant de modéliser une grande quantité d'effets en choisissant/combinant correctement la/les fonction(s) tridimentionnelle(s) associée(s). De plus on est indépendant de la topologie de la surface. Le rendu est par contre très lent.
5.10 Animations
On peut maintenant créer des animations avec les images obtenues par ray-tracing. La création de ces animation est évidemment très longue par cette méthode. Elles consistent à réaliser le rendu de multiples images en modifiant un paramètre de temps.
Par exemple pour réaliser une translation le long de l'axe x, il suffit de remplacer x par x−clock. Et pour obtenir une modification de la forme de la vague, il suffit de translater la fonction de bruit le long de l'axe vertical par exemple en remplacant y par y−clock19
Ainsi le calcul de plusieurs images en utilisant la fonction suivante
function { y-0.2-f_normal_perturb(x/4.0-clock, y/4.0-clock, z/4.0)/1.3 }
permet d'obtenir les animations de vagues fournies en annexes.
Ces animations montrent des oscillations qui peuvent sembler être réalistes au premier abord, par contre, une étude plus attentive montre assez rapidement que le mouvement ainsi créé ne correspond pas à une situation réelle.
En effet, de par l'abscence de physique sous jacente à l'animation du bruit, les vagues ne s'influencent pas les une les autres. Ainsi des vagues vont disparaître sans aucun mouvement autour, alors que d'autres vont se créer sans aucune raison particulière.
Si l'utilisation du bruit de Perlin permet de simuler des cas proche du photoréalisme d'une surface liquide, l'animation de celle-ci de façon réaliste n'est pas une chose évidente.
On peut ainsi voir que la physique n'est pas forcément indispensable pour donner un aspect réaliste à la surface elle même, mais c'est pour son évolution que l'on devrait maintenant utiliser les fonctions mises en place dans la première partie de ce rapport. Ces fonctions pourraient alors être modulées par du bruit afin de leur donner un aspect beaucoup plus réaliste et complexe tout en gardant un mouvement physiquement correct.
5.11 Possibilité de lien avec l'aspect physique et difficultés liées
Finalement, après avoir mis en place une méthode “pseudo” physique dans la première partie de ce rapport, et avoir mis en place une méthode de rendu de bonne qualité, il serait interessant d'utiliser ces deux méthodes de façon combinée. On aurait alors accès aux avantages de celles-ci
-
Un rendu de bonne qualité
- Un rendu statique d'aspect complexe et réaliste grâce au bruit de Perlin et à ses variantes.
- Un rendu dynamique réaliste grâce à la prise en compte de la physique et la possibilité de jouer sur la profondeur du sol.
Nous aurions par contre toujours l'inconvénient d'un rendu plutôt lent si celui-ci se réalise par ray-tracing.
Cependant, la synthèse des méthodes n'est pas absolument évidente. En effet, nous avons pu constater que la méthode des isosurfaces fournissait un résultat de bonne qualité et une modularité de la surface importante. Cependant, les équations physiques sont données sous forme paramétriques. On rapelle ici la forme des équations des trochoïdes
Afin de mettre cette équation sous forme implicite, il faudrait arriver à exprimer r0 en fonction de (x,y,z) ce qui n'est pas évident car les équations sont non linéaires et les expressions des solutions ne s'expriment pas sous forme algébriques même pour le cas d'une seule onde.
La méthode utilisant une fonction implicite parraît donc difficile à manipuler si l'on souhaite y ajouter la forme donnée par cette équation paramétrique.
La méthode utilisant les height fields, ne permet évidement pas de mettre en place cette équation car les positions x et y sont fixes.
On peut donc penser à utiliser directement une forme paramétrique. Cependant, l'implémentation directe du rendu d'une équation paramétrique en ray-tracing n'est pas aussi simple que dans le cas du rendu par l'utilisation de vertex comme dans le cas d'OpenGL. Bien que Pov-Ray implémente ce type de rendu, celui çi est encore au stade expérimental, et son utilisation est si lente qu'il rend tout rendu de forme complexe impossible.
Aussi, il semble qu'un compromis doit être réalisé afin de pouvoir mettre en commun les deux approches.
Il semble alors raisonnable de perdre la description de la surface sous forme totalement mathématique et de considérer à nouveau une description sous forme de vertex. Ensuite, les vertex pourraient subir à la fois la déformation due à l'onde physique et due au bruit de Perlin. Enfin le rendu pourrait encore être réalisé sous Pov-Ray qui prend en charge correctement les listes de vertex.
Dans ce cas, les vertex pourraient directement être calculés par des logiciels tels que Matlab, et seule la partie rendu serait réalisée par Pov-Ray.
Cette méthode permet une souplesse maximale au niveau de la déformation des vertex tout en gardant un rendu de bonne qualité pour peu que le nombre de vertex soit suffisant.
Cette étape étant en cours de travail, nous avons d'ores et déjà implémentés une méthode permettant d'exporter des surfaces Matlab en tant que mesh sous Pov-Ray.
On exporte alors la surface sous la forme attendue par Pov sous forme vertex, normal et connectivité.
Un exemple de fichier texte créé et lisible sous Pov-Ray est donné par
#declare surf_test_mesh_1 =
mesh2
{
/* subdivision */
/* vertex_vectors */
/* <Vx,Vy,Vz> */
vertex_vectors
{
160000
#include "lib_data_surf_vertices_test_mesh_1.inc"
}
/* normal_vectors */
/* <Nx,Ny,Nz> */
normal_vectors
{
160000
#include "lib_data_surf_normal_test_mesh_1.inc"
}
/* face_indices */
/* <face1,face2,face3>, index_color_face1,index_color_face2,index_color_face3 */
face_indices
{
318402
#include "lib_data_surf_face_test_mesh_1.inc"
}
}
où chaque liste de vertex, normal et connectivité est donné par le nombre de vecteurs puis la liste de composantes.
Il est alors simple de créer les surfaces trochoïdes sous Matlab et d'en visualiser le résultat sous Pov-Ray. Un exemple est alors montré en fig. 69 où l'on utilise simplement deux ondes.
Fig. 69: [
Exemple de trochoïdes sous Pov-Ray.]Exemple de trochoïdes créés sous Matlab et exportés en tant que mesh sous Pov-Ray.
Il est alors très aisé d'ajouter un bruit de Perlin simple où à crêtes20 sur la surface en déplaçant les vertex directement sous Matlab par le script donné au chapitre précédent. Un exemple d'ajout de bruit de Perlin simple sur la scène précédante est alors montré en fig. 70.
Fig. 70: [
Ajout du bruit de Perlin sur les trochoïdes.]Ajout d'un bruit de Perlin sur les vertex définissant la trochoïde sous Matlab et visualisation par ray tracing.
Le rendu des vagues est correct et possède l'avantage d'être relativement rapide.
On peut complexifier également la scène en mettant en place l'aspect d'une plage en ajoutant un simple sol incliné perturbé par un bruit de Perlin comme montré en fig. 71. On pourrait égalemement mettre en place la dépendant de la relation de dispersion en fonction de la hauteur du sol.
Fig. 71: [
Scène de plage avec une mesh matlab.]Mise en place d'une scène de plage avec l'eau réalisé en mesh sous Matlab.
Enfin, on peut montrer la robustesse de la méthode et sa possiblité d'utilisation dans des domaines très larges en l'appliquant à des mesh plus complexes qu'un simple plan. On utilise alors comme exemple le modèle du lapin bien connu: le bunny de Stanford21 qui est disponible sous forme de fichier ply (liste de vertex suivit de la liste de la connectivité).
Le fichier de la surface est alors lu sous Matlab et exporté sous Pov-Ray par la méthode utilisée précédemment. Un exemple d'affichage de la surface et d'application sur bruit de Perlin sur celle-ci est alors illustré en fig. 72.
Fig. 72: [
Visualisation du lapin sous Pov-Ray et application du bruit.]Visualisation du lapin sous Pov-Ray avec une simple couleur rouge. La première image montre la surface originale alors que la seconde image est réalisée en ajoutant un bruit de Perlin sur les vertex.
Dans cette figure, nous avons uniquement appliqué une couleur rouge opaque. Il est cependant aisé de leur appliquer la couleur transparente utilisé pour l'eau. On obtient alors pour les deux figures précédentes celles montrées en fig. 73.
Fig. 73: [
Lapin visualisé par une texture d'aspect liquide.]Visualisation des deux lapins de la fig. 72 avec une texture transparente.
On peux évidemment mettre ce lapin dans un décors comme montré en fig. 74 dans un cas très simple.
Fig. 74: [
Lapin placé dans une scène]Lapin en couleur transparente mise dans une scène.
Il serait enfin possible de mettre en place une animation, cependant, il faudrait charger une mesh différente pour chaque frame. Il faut exporter une surface différente et la recharger à chaque affichage.
Cela peut notamment prendre une place non négligeable sur le disque. En effet, le stockage des vertex se réalisant en ASCII non compressé, un fichier total de description d'une scène peut prendre rapidement une dizaine de méga. Ainsi, une scène animée d'une centaine d'images devrait prendre rapidement une place de l'ordre du giga de données. Cela reste cependant tout à fait réalisable avec la taille des disques durs actuels.
5.12 En Résumé
-
L'animation par ray-tracing est possible en réalisant le rendu de nombreuses images mais prend un temps conséquent.
- L'animation utilisant seulement un bruit non physique manque de réalisme. Mais l'ajout du modèle physique est difficile à mettre en place par la méthode d'isosurface.
- Une possibilité de lien physique et bruit est possible en réalisant simplement la déformation sur une mesh puis en en faisant le rendu par ray-tracing.
6 Discussion et Conclusion
6.1 Discussion
La première partie du rapport a montré que de se baser totalement sur la physique du phénomène afin de donner un aspect visuel correct n'est pas une chose aisée. En effet, bien que les équations de bases soient bien connues, celles-ci sont de loin bien trop compliquées pour en obtenir une visualisation tridimentionnelle en un temps raisonnable (et encore moins en temps réel).
Nous avons suivi un schéma de simplification basé sur des hypothèses et notamment sur une linéarisation permettant de simplifier très fortement les équations et du même temps de limiter de beaucoup l'application du résultat aux cas de très faibles amplitudes.
Les vagues que nous souhaitions visualiser sont donc déjà en théorie en dehors de l'approximation.
Le modèle a pu ensuite être complexifié légèrement en prenant en compte la hauteur du sol afin de modifier la vitesse de déplacement de chaque onde.
Lors de l'implémentation, nous nous sommes confrontés à des difficultés notamment pour le choix des amplitudes et des directions des ondes afin de donner un aspect réaliste. En effet, l'ajout de nombreux vecteurs d'ondes de fréquences proches nous donnaient généralement un simple paquet d'onde traversant la surface ce qui n'était pas le but recherché. De plus nous ne souhaitions pas choisir une amplitude trop faible afin d'éviter d'avoir de simple sinusoïdes, mais le choix d'une amplitude un peu trop grande rendait la fonction moins réaliste et notamment le risque d'avoir un phénomène de croisement des vertex lorsque la déformation en abscisse devenait trop importante.
De nombreux tests de choix d'amplitudes et de train d'ondes on ainsi du être réalisés sous Matlab en mode unidimentionnel avant de l'implémenter sous OpenGL.
Normalement, ces trains d'ondes auraient du être choisis suivant une distribution fréquentielle donnée par la vitesse du vent [18].
Le modèle dépendant de la hauteur du sol a également posé quelques difficultées, notamment si l'on souhaite bien visualiser l'effet du sol, il est nécessaire de rapprocher celui-ci de la surface. Cependant, lorsque le sol est trop proche des vagues, un phénomène de “bouchon” se forme sur le bord et se propage vers l'arrière. Le phénomène n'apparaît pas très naturel mais il est par contre du à la limitation même des approximations physiques réalisées pour obtenir l'équation.
Nous avons donc pu visualiser que, comme annoncé dans l'introduction, la visualisation de surface liquide liée à la physique est complexe car elle nécessite, pour obtenir une visualisation convainquante, de ne pas réaliser d'approximations trop importantes (notamment au niveau des linéarisations). Si le calcul de la valeur d'une pression sur une paroie se trouvera peut être peu modifiée par une linéarisation dans lequel le modèle colle correctement, la visualisation de la surface quand à elle en est profondément affectée car notre impression de réalisme d'une scène est surtout sensible aux phénomènes non linéaires.
La seconde partie du rapport concernant la mise en place du bruit de Perlin a permit notamment d'entrevoir l'étendue impressionnante de l'application de ce bruit. Dans le même temps, nous avons été étonnés par la simplicité du concept en lui même.
L'implémentation sous OpenGL du bruit n'a pas posé de soucis particuliers. On pourra toutefois noter que nous avons initialement implémentés le bruit avec la méthode d'interpolation sinusoïdale. Or cette méthode, bien que donnant des résultats corrects pour une image fixe, donne un effet d'accélération et de décélération périodique lors de l'animation due à la tangente nulle pour chaque valeur entière. Nous avons mis un certain temps à comprendre d'où provenait ce problème que l'on a pu résoudre par l'interpolation tricubique. Celle-ci pose cependant ses propres problèmes car elle ralentie de façon considérable le calcul et la plupart des tests on du être réalisés par une interpolation de type sinusoïdale (plus rapide même avec notre implémentation peu optimisée, car les valeurs du sinus ne sont pas précalculées dans un vecteur).
La recherche et la compréhension du bruit de Perlin à crêtes à par contre été plus délicate. En effet, ce bruit est souvent mentionné sur Internet, par contre les explications sont souvent limitées au bruit de Perlin classique et seul les résultats donnés par le bruit à crêtes sont montrés. La formule de calcul n'est donc pas facile à obtenir et peu de littérature semble en faire mention. Nous avons donc due utiliser directement le code source de Pov-Ray afin d'essayer de comprendre la formule implémentée. Le code source n'est malheureusement pas immédiat à comprendre, en effet les noms de variables choisis sont assez peu explicites (ex. ea pour signifier exponential array,...) et le programme en lui même étant conséquent, les nombreux appels aux différentes fonctions n'ont pas étés immédiats à comprendre. Le code mentionnait que la formule implémentée était tiré de la ref. [27].
La dernière partie du rapport faisant suite à celle du bruit s'est interessée au rendu par la technique de ray-tracing avec l'utilisation du logiciel Pov-Ray.
Ce choix s'est réalisé par sa disponibilité et son état de logiciel open source et libre. De plus, l'un des auteurs était déjà familiarisé par l'utilisation de ce logiciel depuis plus de trois ans, l'avais utilisé à plusieurs occasions, et pense que son potentiel pour créer des images d'un rendu de grande qualité permet de rendre certaine visualisation beaucoup plus attrayantes.
La première difficulté a été de trouver la combinaison adéquate de la coloration de la surface afin d'obtenir une impression de liquide. Les tutoriaux de Christoff Hormann ont notamment étés d'une grande aide afin de régler ces paramètres (coloration, transparence, reflexion, refraction, ...).
L'utilisation du bruit de Perlin à crêtes (puis seulement ensuite du bruit de Perlin simple dans l'ordre chronologique) a notamment été inspiré par une image de Ben Weston également réalisée sous Pov-Ray.
Cependant, après avoir réglé correctement ces paramètres, nous avons étés surpris nous même par l'aspect réaliste de certaines des images ainsi rendues.
La réelle difficulté a été les très longs tatonnements sur l'ensemble de ces paramètres pour obtenir une surface d'aspect et de couleur réaliste. Ces tatonnements22 sont notamment difficile de par la nature très lente des rendus généralement réalisés tout d'abord en très faible résolution (100× 100) ou il est difficile de voir les détails.
La gestion du temps à ainsi été délicate à gérer pour cette partie. Le plus difficile étant le cas des animations où les calculs de plus de 20 heures pour les animations les plus longues nous obligent à bien choisir les paramètres (notamment la gestion de la déformation de la surface au cours du temps) car il est difficile de se faire une idée de l'aspect de l'animation à vitesse réelle lorsque l'on à pu visualiser qu'un faible nombre d'images avant le lancement réel de l'animation23.
6.2 Travail Future
De nombreuses pistes sont maintenant ouvertes par le travail ainsi débuté. Tout d'abord, le travail ne concerne que la petite partie de la visualisation de fluide traitant de l'aspect des vagues. D'autres domaines peuvent être étudiés comme notamment l'étude de la forme et de l'interaction des gouttes d'eau qui tombe dans un liquide ou sur une surface solide. De nombreux articles sont notamment dédiés au sujet.
Une méthode de propagation d'ondelettes sur une surface liquide à l'aide d'un noyau convolutif expliqué en [30] avait notamment attiré notre attention. Cependant notre tentative d'implémentation ne s'est pas révélée concluante et nous n'avons pas eu le loisir d'approfondir notre recherche jusqu'à maintenant. Il pourrait cependant être interessant d'inclure des effets d'ondelettes sur notre surface bruitée afin de lui donner un aspect plus réaliste24.
Nous souhaiterions également approfondire la partie physique de la modélisation afin de pouvoir appliquer le modèle paramétrique sur des cas plus généraux. Le but serait alors de pouvoir modéliser l'approche des vagues sur la plage comme le montre la ref.[31]. Nous souhaiterions également implémenter le calcul automatique des vecteurs d'ondes et leur modifications aléatoires au cours du temps suivant la distribution en fréquence donné par le vent ce qui permetterais de rendre le programme plus indépendant du choix du codeur et un comportement d'aspect probablement plus réaliste qu'un codage en dur des directions choisies.
Dans un autre domaine, nous voudrions également étudier plus en détail la visualisation possible dans le cas beaucoup plus physique de la résolution directe des équations aux dérivés partielles par des méthodes numériques. C'est évidemment dans cette voie que les modèles de fluides vont pouvoir interagir avec des éléments exterieurs. Des equations relativement “simples” comme celle de l'eau de surface [32, 33] (“shallow water equation”) semble un bon point de départ car cette équation bien que simplifiée est d'ores et déjà non linéaire et modélise la formation des crêtes sur les vagues.
Des méthodes de résolutions par volume fini ou par méthode implicite en différence finie devraient probablement pouvoir donner des résultats intéressant. Les résultats seraient par contre évidemment tous précalculés et il n'est pas encore question de réaliser cela en temps réel.
Une application mélangeant résolution par différence finie et bruit de Perlin à notamment été présenté en [34].
Enfin, et c'est dans cette optique que ce travail avait été réalisé, nous souhaiterions mettre en place réelement le lien entre l'aspect basé sur la physique et celui basé uniquement sur le bruit, notamment dans le cas du rendu par ray-tracing afin d'avoir des animations possèdants des mouvements d'aspects réalistes.
L'implémentation dans le cas d'OpenGL ne poserait pas de problème particuliers et ce sera probablement à partir de cela que nos tests seront réalisés. Le but étant ensuite de le passer sous Pov-Ray. La difficulté de ce passage a notamment été expliqué au chap. 5.11. Cependant, le passage par Matlab pour la création des vertex et l'exportation de ceux-ci au format Pov-Ray est d'ores et déjà implémenté. Il reste donc principalement une phase de test à mettre en oeuvre (pouvant parfois se révéler longue).
6.3 Conclusion
Nous avons donc pu voir que grâce à la simplification des équations générales, aux conséquences parfois lourdes sur le domaine de validité de la solution, permettait d'obtenir des équations facilement implémentables en temps réel sous OpenGL. Cela fournit une visualisation certe simple mais tout à fait raisonnable en terme de réalisme lorsque les conditions de validité sont bien respectées. La mise en place de ces équations ne demande pas beaucoup de calculs suplémentaires par rapport à la mise en place d'un simple sinus sur l'axe verticale et permet par contre d'avoir un mouvement en accord avec la physique du phénomène.
Des petits ajouts tels que l'interaction avec la hauteur du fond permettent notamment, pour un coup assez faible, d'ajouter un niveau de réalisme supplémentaire sans devoir chercher des astuces complexe à mettre en place comme ce serait le cas pour une approche “ad-hoc”.
Cette volonté d'avoir une part de physique derrière le modèle permet donc évidemment d'obtenir des visualisations robustes pour lesquelles on peut s'appuyer pour construire des scènes plus complexes tant que l'on reste à l'intérieur leur domaine de validité.
Cependant, on peut constater que ces modèles restent simples, les vagues restent très lisses et leur comportements ne présentent pas certains effets interessants auxquels on peut s'attendre sur un vrai liquide. La plupart de ces limitations étant notamment due à la prise en compte uniquement de la partie linéaire des équations25. On a alors pu voir qu'une apparente complexité peut être générée à moindre frais par l'utilisation d'un bruit fondamental dans le domaine de la synthèse d'image: le bruit de Perlin.
L'utilisation de ce bruit est l'une de ces variante pris en exemple (bruit de Perlin à crêtes) sont des bruits continus de nature fractale permettant de donner un aspect réaliste très rapidement à une surface.
Ce bruit a été implémenté en temps réel sous OpenGL en déplaçant les vertex de façon simple. Il a cependant été montré que pour une utilisation optimale de la variante à crêtes pemettant de modéliser une forme de vague assez réaliste, le nombre de vertex associé à la crête devait être important. Le bruit doit donc être calculé de façon extrèmement rapide, et pour cela, l'utilisation des shaders des cartes graphiques vont permettre une utilisation plus poussée que celle implémentée.
Enfin, dans la dernière partie, une visualisation de bonne qualité à été réalisée par ray-tracing avec l'utilisation du logiciel open source Pov-Ray. La visualisation de la surface est assez proche d'un aspect réaliste et les différents bruits permettent de modéliser assez fidèlement l'aspect d'un lac ou d'une rivière pour le bruit de Perlin simple, alors que le bruit de Perlin à crêtes donne l'impression de vagues que l'on peut rencontrer sur un océan.
La mise en place d'animations en prenant uniquement ces bruits montre cependant que l'aspect physique est manquant de part l'abscence d'interactions des vagues les unes par rapport aux autres.
On peut ainsi conclure que pour la création d'une image réaliste simple, un bruit de Perlin ou l'une de ses variante associée à un rendu de bonne qualité permet de donner une allure tout à fait convainquante et que le lien avec la physique n'est pas obligatoire. Par contre, pour l'utilisation de séquences animées d'allure réalistes, les interactions et les déformations doivent se faire en accord avec la physique sous jacente. L'utilisation combinée du bruit et des équations simplifiées permettrait alors d'obtenir une animation convainquante de la surface liquide elle même. Cette combinaison permettrait d'obtenir un mouvement simple mais physiquement cohérent et un aspect de complexité donnant une allure réaliste bien que non liée aux équations.
Et enfin, la mise en place d'interaction avec des éléments exterieurs, qui n'a pas été étudié ici, nécessiterait quant à elle une résolution plus complexe des équations aux dérivés partielles afin de tenir compte des conditions frontières non triviales.
Références
- [1]
-
Richard Keiser, Bart Adams, Dominique Gasser, Paolo Bazzi, Philip Dutré, and
Markus Gross.
A unified Lagrangian approach to solid-fluid animation.
The Eurographics Symposium on Point-Based Graphics,
pages 125–148, June 2005.
- [2]
-
Adam W. Bargteil, Tolga G. Goktekin, James F. O'Brien, and John A. Strain.
A semi-Lagrangian contouring method for fluid simulation.
ACM Transactions on Graphics, 25(1):19–38, January
2006.
- [3]
-
Nuttapong Chentanez, Tolga G. Goktekin, Bryan E. Feldman, and James F. O'Brien.
Simultaneous coupling of fluids and deformable bodies.
ACM SIGGRAPH/Eurographics Symposium on Computer
Animation, pages 2 – 4, 2006.
- [4]
-
Bryan E. Feldman, James F. O'Brien, Bryan M. Klingner, and Tolga G. Goktekin.
Fluids in deforming meshes.
ACM SIGGRAPH/Eurographics Symposium on Computer
Animation, pages 255–259, July 2005.
- [5]
-
S. Osher and J. Sethian.
Fronts propagating with curvature dependent speed: Algorithms based
on Hamilton-Jacobi formulations.
Journal of Computerized Physics, 79:12–49, 1988.
- [6]
-
Stanley Osher and Ronald Fedkiw.
Level Set Methods and Dynamic Implicit Surfaces.
Springer, 2003.
- [7]
-
Nick Foster and Ronald Fedkiw.
Practical animation of liquids.
SIGGRAPH '01: Proceedings of the 28th annual conference on
Computer graphics and interactive techniques, pages 23–30, 2001.
- [8]
-
K. W. Morton and D. F. Mayers.
Numerical Solution of Partial Differential Equations.
Cambridge, 2005.
- [9]
-
James W. Thomas.
Numerical Partial Differential Equations. Finite Difference
Methods.
Springer, 1995.
- [10]
-
Howard Elman, David Silvester, and Andy Wathen.
Finite Elements and Fast Iterative Solvers, with Applications in
Incompressible Fluid Dynamics.
Oxford Science, 2005.
- [11]
-
Dietrich Braess.
Finite Elements. Teory, Fast Solvers, and Applications in
Solid Mechanics.
Cambridge, 2001.
- [12]
-
Damien Hinsinger, Marie-Paule Cani, and Fabrice Neyrat.
Interactive animation of ocean waves.
In ACM-SIGGRAPH/EG Symposium on Computer Animation (SCA),
July 2002.
- [13]
-
Damien Hinsinger, Marie-Paule Cani, and Fabrice Neyret.
Modélisation et animation de la mer en temps réel.
Technical Report, INRIA groupe EVASION, ENSIMAG,
June 2001.
- [14]
-
Jean-Christophe Gonzato and Bertrand Le Saëc.
A phenomenological model of coastal scenes based on physical
considerations.
8th Eurographics Workshop on Computer Animation and
Simulation, pages 137–148, 1997.
- [15]
-
Jean-Christophe Gonzato.
Modélisation des scènes océaniques.
PhD thesis, December 1999.
- [16]
-
Jerry Tessendorf.
Simulating ocean water.
SIGGRAPH course notes, Simulating Nature: Realistic and
Interactive Techniques Course Notes, 1999.
- [17]
-
Stefan Jeschke, Hermann Birkholz, and Heidrun Schmann.
A procedural model for interactive animation of breaking ocean waves.
WSCG, February 2003.
- [18]
-
Sébastien Thon, Jean-Michel Dischler, and Djamchid Ghazanfarpour.
Synthèse de vagues d'océan par étude spectrale.
Actes des 12èmes journées AFIG, pages 235–243, 1999.
- [19]
-
Jason L. Mitchell.
Real-time synthesis and rendering of ocean water.
ATI Research Technical Report, April 2005.
- [20]
-
Simon Premoze and Michael Ashikhmin.
Rendering natural waters.
8th Pacific Conference on Computer Graphics and Applications,
October 2000.
- [21]
-
Ken Perlin.
Hypertexture.
Computer Graphics, 23(3):253–262, July 1989.
- [22]
-
Alfio Quarteroni, Riccardo Sacco, and Fausto Saleri.
Numerical Mathematics.
Springer, 1991.
- [23]
-
Carl de Boor.
A Practical Guide to Splines.
Springer, 2001.
- [24]
-
W. E. Lorensen and H. E. Cline.
Marching Cubes : A high resolution 3D surface construction
algorithm.
SIGGRAPH '87:, 21(4):163–169, July 1987.
- [25]
-
S. Thon, J.M. Dischler, and D. Ghazanfarpour.
A simple model for visually realistic running waters.
18th Eurographics UK proceedings, EGUK'00, pages 81–86,
2000.
- [26]
-
Heinz-Otto Peitgen, Hans-Otto Peitgen, and Hartmut Juergens.
Chaos and Fractals: New Frontiers of Science.
Springer, 2004.
- [27]
-
David S. Ebert, F. Kenton Musgrave, Darwyn Peachey, Ken Perlin, and Steven
Worley.
Texturing and Modeling: A Procedural Approach.
Morgan Kaufmann, 2002.
- [28]
-
Lionel Baboud and Xavier Décoret.
Realistic water volumes in real-time.
Eurographics Workshop on Natural Phenomena, pages 1–8,
2006.
- [29]
-
S. Thon and D. Ghazanfarpour.
Animation de l'eau en synthèse d'images : exemple de cours d'eau.
July 2001.
- [30]
-
J. Loviscach.
A convolution-base algorithm for animated water waves.
Eurographics, pages 383–389, 2002.
- [31]
-
Alain Fournier and William T. Reeves.
A simple model of ocean waves.
SIGGRAPH '86, 20:75–84, August 1986.
- [32]
-
Randall J. Leveque.
Finite Volume Methods for Hyperbolic Problems.
Cambridge, 2003.
- [33]
-
Stephen Roberts and Christopher Zoppou.
Robust and efficient solution of the 2D shallow water equation with
domains containing dry beds.
Australian and New Zealand Industrial and Applied
Mathematics, 42:1260–1282, 2000.
- [34]
-
S. Thon and D. Ghazanfarpour.
A semi-physical model of running water.
19th Eurographics UK proceedings, EGUK'01, 53–59, 2001.
- 1
- intérmédiaire
- 2
- La condition d'incompressibiilité rend le problème “stiff” (raide) et numériquement instable
- 3
- On pourrait également essayer d'autres types de distributions de bruit, cela pourrait certainement donner d'autres types d'applications pour le bruit de Perlin en fournissant des allures différentes.
- 4
- pour éviter d'avoir toujours les mêmes valeurs
- 5
- Ce qui augmente fortement le nombre d'appel de fonction, notamment pour le cas 3D
- 6
- réduit donc un nombre important d'appel de fonctions
- 7
- il faut dans ce cas prendre en compte l'ensemble des sommets du cube entourant le point plus les sommets de tous les cubes voisins, ce qui fourni 64 sommets
- 8
- avec ∥f∥∞=maxx∈RN ∥f(x)∥
- 9
- Le résultat sera plus précis que sur une approche basée sur des différences finies
- 10
- On préfèrera le multitexturing par rapport au blending simple car la surface ne sera calculé et envoyé dans le pipe-line de rendu qu'une seule fois.
- 11
- La sky box utilisé prise du site http://cubed.shadowpuppet.net/index.html
- 12
- Exemples créés lors d'une présentation de première année.
- 13
- dont nous ne disposons pas
- 14
- Nous metterons ainsi en place à la fin une possibilité d'exporter des surfaces Matlab vers Pov-Ray
- 15
- dans le cas contraire, on voit le sol apparaitre à l'horizon.
- 16
- Les images dans l'exemple sont rendues en 1280× 960 avec antialiasiasing en moins de 2 minutes.
- 17
- Des utilisations classiques conçus spécialement pour ces effets et basées sur des sphéres sont les blobs ou les metaballs.
- 18
- on pourrait également penser à une fonction paramétrique sur les trois coordonnées.
- 19
- Pov-Ray utilise un système d'axe non direct et y correspond à l'axe vertical.
- 20
- Celui-ci est limité par la taille de la mesh.
- 21
- Disponible sur http://graphics.stanford.edu/data/3Dscanrep/
- 22
- Lors du rendu des premières images, le comportement de chaque paramètre du bruit de Perlin à crêtes étaient encore mal compris.
- 23
- Générallement lancé pendant toute la nuit, ce qui nécessite donc d'avoir la scène parfaitement prête le soir même.
- 24
- notamment en cas de pluie
- 25
- Cela constitue généralement l'unique moyen d'obtenir une solution algébrique.
Ce document a été traduit de LATEX par HEVEA