Imagine Internships

(2011-2012)


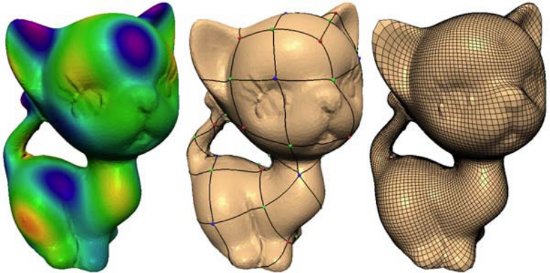
Figure 1 extracted from reference [1]: Left the Laplacian on a triangular mesh, Middle the Morse-Smale complex, Right a quadragulation of the triangular mesh.

Advisors

Georges-Pierre Bonneau, Maverick/LJK team
Stefanie Hahmann, IMAGINE team
Vijay Natarajan, IISc Bangalore

Contact: Stefanie.Hahmann@inria.fr

Subject

Morse-smale complexes are topological structures related to functions on manifolds. In 2D, they form quad-cells that have been used with success in Computer Graphics in order to quadrangulate complex surfaces ([1] and Figure 1). Morse-Small complexes have also been used in Visualization in order to capture in one image the global behaviour of large scientific datasets ([2,3] and Figure 2). For noisy data, Morse-Small complexes exhibit unwanted and unnecessary nodes and cells that must be simplified. Previous works have developed combinatorial techniques to perform this simplification. Until now very few works have looked at the design of new functions conforming to the simplified structures. Applications include smoothing of surfaces as well as topology preserving smoothing and visualization of datasets. In [3] the authors have to solve a laplacian system in order to compute new functions on the simplfied Morse-Smale complex. This relies in a time-consuming algorithm. In collaboration with Prof. Vijay Natarajan ([4)] from the IISc, Bangalore, we want to investigate more efficient techniques inspired by earlier works in the field of Computer Aided Geometric Design. Our goal is to efficiently and robustly design new functions from a given set of simplified Morse-Smale complexes.

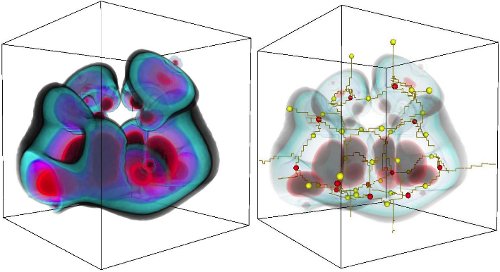
Figure 2 extracted from reference [2]: Left a volumetric dataset, Right the Morse-Smale complex connecting local maxima (in red) and 2-saddles (in yellow).

References

[1] Shen Dong, Peer-Timo Bremer, Michael Garland, Valerio Pascucci, and John C. Hart. 2006. Spectral surface quadrangulation. In ACM SIGGRAPH 2006 Papers (SIGGRAPH '06). ACM, New York, NY, USA, 1057-1066
[2] Attila Gyulassy, Vijay Natarajan, Valerio Pascucci, Bernd Hamann, "Efficient Computation of Morse-Smale Complexes for Three-dimensional Scalar Functions," IEEE Transactions on Visualization and Computer Graphics, pp. 1440-1447, November/December, 2007
[3] T. Weinkauf, Y. Gingold, O. Sorkine. Topology-based Smoothing of 2D Scalar Fields with C1-Continuity Computer Graphics Forum (Proc. EuroVis) 29(3), June 2010
[4] Homepage of Prof. Vijay Natarajan