Imagine Internships

(2011-2012)

Advisors

Stefanie Hahmann, IMAGINE team
Luc Biard, MGMI/LJK
Nicolas Szafran, MGMI/LJK

Contact: Stefanie.Hahmann@inria.fr

Context and Objective

A developable surface is a surface, which can be unfolded (developed) into a plane without stretching or tearing. Because of this property, developable surfaces possess a variety of applications in manufacturing with materials that are not amenable to stretching (leather for shoes or hand bags, skins of aircrafts, sails). In computer graphics developable surfaces are very popular to model, simulate or animate clothes or folded papers in virtual environments.
Existent algorithms optimize a triangular surface mesh following some non-linear criteria in order to converge to a quasi-developable surface. Others reconstruct a developable triangle surface mesh from some given arbitrary boundary curves using a branch & bound approach. These approaches are very time consuming.
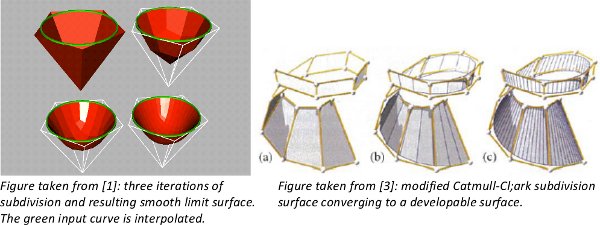
The goal of the M2 project is to develop a new method, which takes as input not only a set of boundary curves, but also tangent planes along these curves. Both, curves and tangent planes are supposed to belong to a developable surface. Our approach is based on a hierarchical surfaces construction. Similar to standard subdivision surface algorithms [1,2] we start with a very coarse grid, and compute a series of refined developable grids, which at the end results in a smooth developable surface.

Work plan

Study first relevant literature on subdivision surfaces [1,2] and on developable surface approximation algorithms [3,4]. Propose and implement at least one algorithm computing the hierarchy of developable grids. Choose a geometric criterion to ensure developability of the grids. Apply your criterion at each grid level.

2 options are possible

• it is possible to extend your method to time-varying (animated) input data in order to compute a deforming developable surface.
• it is possible to study geometrical properties of the proposed new surface scheme

The whole project is a "math-info" project. It can either be oriented more to computer graphics or to applied mathematics aspects.

References

[1] Adi Levin: Interpolating nets of curves by smooth subdivision surfaces, SIGGRAPH'99
http://www.math.tau.ac.il/~levin/adi/paper7.htm
[2] Adi Levin: Combined Subdivision Schemes for the design of surfaces satisfying boundary conditions , CAGD 16, (1999)
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.16.4022
[3] Liu, Potmann et al. : SIGGRAPH'06
http://www.geometrie.tugraz.at/wallner/quad06.pdf
[4] C. Wang: Flattenable Mesh Surface Fitting on Boundary Curves
http://www2.mae.cuhk.edu.hk/~cwang/pubs/ASMEFLFitting.pdf